Basic concepts of the homography explained with code

Table of Contents

• Introduction
  • Basic theory
    • What is the homography matrix?
    • How the homography transformation can be useful?
  • Demonstration codes
    • Demo 1: Pose estimation from coplanar points
    • Demo 2: Perspective correction
    • Demo 3: Homography from the camera displacement
      • Exercise
    • Demo 4: Decompose the homography matrix
    • Demo 5: Basic panorama stitching from a rotating camera
  • Additional references

Prev Tutorial: AKAZE and ORB planar tracking

Compatibility	OpenCV >= 3.0

Introduction

This tutorial will demonstrate the basic concepts of the homography with some codes. For detailed explanations about the theory, please refer to a computer vision course or a computer vision book, e.g.:

• Multiple View Geometry in Computer Vision, Richard Hartley and Andrew Zisserman, [117] (some sample chapters are available here, CVPR Tutorials are available here)
• An Invitation to 3-D Vision: From Images to Geometric Models, Yi Ma, Stefano Soatto, Jana Kosecka, and S. Shankar Sastry, [178] (a computer vision book handout is available here)
• Computer Vision: Algorithms and Applications, Richard Szeliski, [260] (an electronic version is available here)
• Deeper understanding of the homography decomposition for vision-based control, Ezio Malis, Manuel Vargas, [181] (open access here)
• Pose Estimation for Augmented Reality: A Hands-On Survey, Eric Marchand, Hideaki Uchiyama, Fabien Spindler, [183] (open access here)

The tutorial code can be found here C++, Python, Java. The images used in this tutorial can be found here (left*.jpg).

Basic theory

What is the homography matrix?

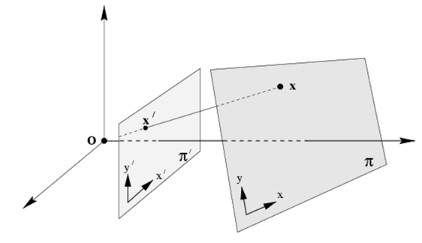
Briefly, the planar homography relates the transformation between two planes (up to a scale factor):

\[ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = \mathbf{H} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

The homography matrix is a 3x3 matrix but with 8 DoF (degrees of freedom) as it is estimated up to a scale. It is generally normalized (see also 1) with \( h_{33} = 1 \) or \( h_{11}^2 + h_{12}^2 + h_{13}^2 + h_{21}^2 + h_{22}^2 + h_{23}^2 + h_{31}^2 + h_{32}^2 + h_{33}^2 = 1 \).

The following examples show different kinds of transformation but all relate a transformation between two planes.

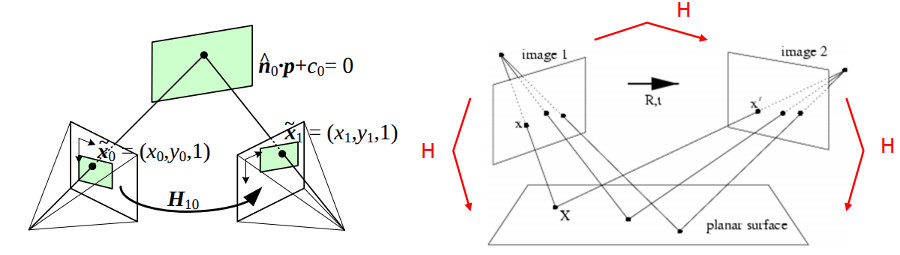
• a planar surface and the image plane (image taken from 2)

• a planar surface viewed by two camera positions (images taken from 3 and 2)

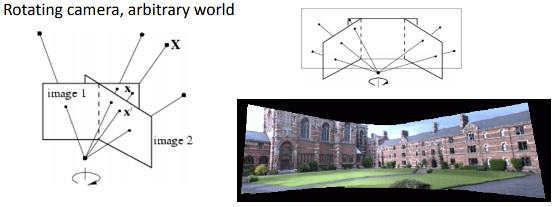
• a rotating camera around its axis of projection, equivalent to consider that the points are on a plane at infinity (image taken from 2)

How the homography transformation can be useful?

• Camera pose estimation from coplanar points for augmented reality with marker for instance (see the previous first example)

• Perspective removal / correction (see the previous second example)

• Panorama stitching (see the previous second and third example)

Demonstration codes

Demo 1: Pose estimation from coplanar points

Note

Please note that the code to estimate the camera pose from the homography is an example and you should use instead cv::solvePnP if you want to estimate the camera pose for a planar or an arbitrary object.

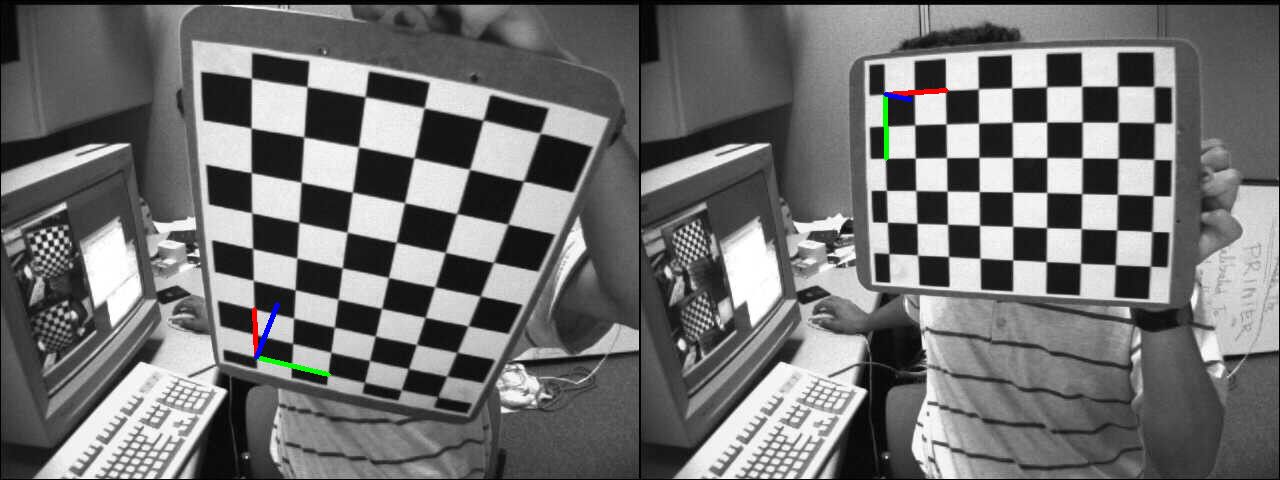
The homography can be estimated using for instance the Direct Linear Transform (DLT) algorithm (see 1 for more information). As the object is planar, the transformation between points expressed in the object frame and projected points into the image plane expressed in the normalized camera frame is a homography. Only because the object is planar, the camera pose can be retrieved from the homography, assuming the camera intrinsic parameters are known (see 2 or 4). This can be tested easily using a chessboard object and findChessboardCorners() to get the corner locations in the image.

The first thing consists to detect the chessboard corners, the chessboard size (patternSize), here 9x6, is required:

    vector<Point2f> corners;
    bool found = findChessboardCorners(img, patternSize, corners);

The object points expressed in the object frame can be computed easily knowing the size of a chessboard square:

        for( int i = 0; i < boardSize.height; i++ )
            for( int j = 0; j < boardSize.width; j++ )
                corners.push_back(Point3f(float(j*squareSize),
                                          float(i*squareSize), 0));

The coordinate Z=0 must be removed for the homography estimation part:

    vector<Point3f> objectPoints;
    calcChessboardCorners(patternSize, squareSize, objectPoints);
    vector<Point2f> objectPointsPlanar;
    for (size_t i = 0; i < objectPoints.size(); i++)
    {
        objectPointsPlanar.push_back(Point2f(objectPoints[i].x, objectPoints[i].y));
    }

The image points expressed in the normalized camera can be computed from the corner points and by applying a reverse perspective transformation using the camera intrinsics and the distortion coefficients:

    FileStorage fs( samples::findFile( intrinsicsPath ), FileStorage::READ);
    Mat cameraMatrix, distCoeffs;
    fs["camera_matrix"] >> cameraMatrix;
    fs["distortion_coefficients"] >> distCoeffs;

    vector<Point2f> imagePoints;
    undistortPoints(corners, imagePoints, cameraMatrix, distCoeffs);

The homography can then be estimated with:

    Mat H = findHomography(objectPointsPlanar, imagePoints);
    cout << "H:\n" << H << endl;

A quick solution to retrieve the pose from the homography matrix is (see 5):

    // Normalization to ensure that ||c1|| = 1
    double norm = sqrt(H.at<double>(0,0)*H.at<double>(0,0) +
                       H.at<double>(1,0)*H.at<double>(1,0) +
                       H.at<double>(2,0)*H.at<double>(2,0));
 
    H /= norm;
    Mat c1  = H.col(0);
    Mat c2  = H.col(1);
    Mat c3 = c1.cross(c2);
 
    Mat tvec = H.col(2);
    Mat R(3, 3, CV_64F);
 
    for (int i = 0; i < 3; i++)
    {
        R.at<double>(i,0) = c1.at<double>(i,0);
        R.at<double>(i,1) = c2.at<double>(i,0);
        R.at<double>(i,2) = c3.at<double>(i,0);
    }

\[ \begin{align*} \mathbf{X} &= \left( X, Y, 0, 1 \right ) \\ \mathbf{x} &= \mathbf{P}\mathbf{X} \\ &= \mathbf{K} \left[ \mathbf{r_1} \hspace{0.5em} \mathbf{r_2} \hspace{0.5em} \mathbf{r_3} \hspace{0.5em} \mathbf{t} \right ] \begin{pmatrix} X \\ Y \\ 0 \\ 1 \end{pmatrix} \\ &= \mathbf{K} \left[ \mathbf{r_1} \hspace{0.5em} \mathbf{r_2} \hspace{0.5em} \mathbf{t} \right ] \begin{pmatrix} X \\ Y \\ 1 \end{pmatrix} \\ &= \mathbf{H} \begin{pmatrix} X \\ Y \\ 1 \end{pmatrix} \end{align*} \]

\[ \begin{align*} \mathbf{H} &= \lambda \mathbf{K} \left[ \mathbf{r_1} \hspace{0.5em} \mathbf{r_2} \hspace{0.5em} \mathbf{t} \right ] \\ \mathbf{K}^{-1} \mathbf{H} &= \lambda \left[ \mathbf{r_1} \hspace{0.5em} \mathbf{r_2} \hspace{0.5em} \mathbf{t} \right ] \\ \mathbf{P} &= \mathbf{K} \left[ \mathbf{r_1} \hspace{0.5em} \mathbf{r_2} \hspace{0.5em} \left( \mathbf{r_1} \times \mathbf{r_2} \right ) \hspace{0.5em} \mathbf{t} \right ] \end{align*} \]

This is a quick solution (see also 2) as this does not ensure that the resulting rotation matrix will be orthogonal and the scale is estimated roughly by normalize the first column to 1.

A solution to have a proper rotation matrix (with the properties of a rotation matrix) consists to apply a polar decomposition, or orthogonalization of the rotation matrix (see 6 or 7 or 8 or 9 for some information):

    cout << "R (before polar decomposition):\n" << R << "\ndet(R): " << determinant(R) << endl;
    Mat_<double> W, U, Vt;
    SVDecomp(R, W, U, Vt);
    R = U*Vt;
    double det = determinant(R);
    if (det < 0)
    {
        Vt.at<double>(2,0) *= -1;
        Vt.at<double>(2,1) *= -1;
        Vt.at<double>(2,2) *= -1;
 
        R = U*Vt;
    }
    cout << "R (after polar decomposition):\n" << R << "\ndet(R): " << determinant(R) << endl;

To check the result, the object frame projected into the image with the estimated camera pose is displayed:

Demo 2: Perspective correction

In this example, a source image will be transformed into a desired perspective view by computing the homography that maps the source points into the desired points. The following image shows the source image (left) and the chessboard view that we want to transform into the desired chessboard view (right).

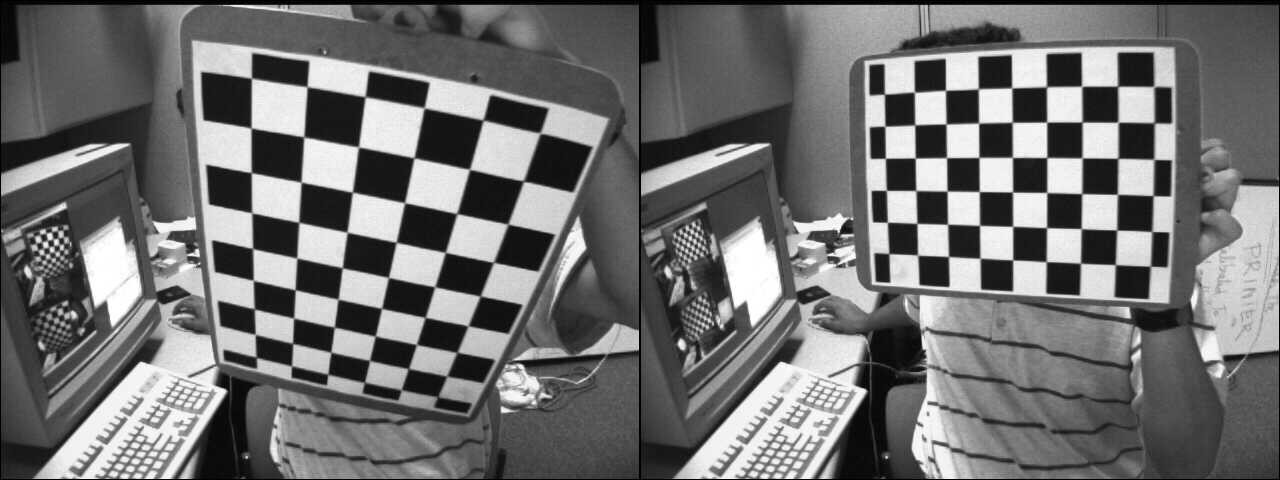
Source and desired views

The first step consists to detect the chessboard corners in the source and desired images:

C++

    vector<Point2f> corners1, corners2;
    bool found1 = findChessboardCorners(img1, patternSize, corners1);
    bool found2 = findChessboardCorners(img2, patternSize, corners2);

Python

    ret1, corners1 = cv.findChessboardCorners(img1, patternSize)
    ret2, corners2 = cv.findChessboardCorners(img2, patternSize)

Java

        MatOfPoint2f corners1 = new MatOfPoint2f(), corners2 = new MatOfPoint2f();
        boolean found1 = Calib3d.findChessboardCorners(img1, new Size(9, 6), corners1 );
        boolean found2 = Calib3d.findChessboardCorners(img2, new Size(9, 6), corners2 );

The homography is estimated easily with:

C++

    Mat H = findHomography(corners1, corners2);
    cout << "H:\n" << H << endl;

Python

    H, _ = cv.findHomography(corners1, corners2)
    print(H)

Java

        Mat H = new Mat();
        H = Calib3d.findHomography(corners1, corners2);
        System.out.println(H.dump());

To warp the source chessboard view into the desired chessboard view, we use cv::warpPerspective

C++

    Mat img1_warp;
    warpPerspective(img1, img1_warp, H, img1.size());

Python

    img1_warp = cv.warpPerspective(img1, H, (img1.shape[1], img1.shape[0]))

Java

        Mat img1_warp = new Mat();
        Imgproc.warpPerspective(img1, img1_warp, H, img1.size());

The result image is:

To compute the coordinates of the source corners transformed by the homography:

C++

    Mat img_draw_matches;
    hconcat(img1, img2, img_draw_matches);
    for (size_t i = 0; i < corners1.size(); i++)
    {
        Mat pt1 = (Mat_<double>(3,1) << corners1[i].x, corners1[i].y, 1);
        Mat pt2 = H * pt1;
        pt2 /= pt2.at<double>(2);
 
        Point end( (int) (img1.cols + pt2.at<double>(0)), (int) pt2.at<double>(1) );
        line(img_draw_matches, corners1[i], end, randomColor(rng), 2);
    }
 
    imshow("Draw matches", img_draw_matches);
    waitKey();

Python

    img_draw_matches = cv.hconcat([img1, img2])
    for i in range(len(corners1)):
        pt1 = np.array([corners1[i][0], corners1[i][1], 1])
        pt1 = pt1.reshape(3, 1)
        pt2 = np.dot(H, pt1)
        pt2 = pt2/pt2[2]
        end = (int(img1.shape[1] + pt2[0]), int(pt2[1]))
        cv.line(img_draw_matches, tuple([int(j) for j in corners1[i]]), end, randomColor(), 2)
 
    cv.imshow("Draw matches", img_draw_matches)
    cv.waitKey(0)

Java

        Mat img_draw_matches = new Mat();
        list2.add(img1);
        list2.add(img2);
        Core.hconcat(list2, img_draw_matches);
        Point []corners1Arr = corners1.toArray();
 
        for (int i = 0 ; i < corners1Arr.length; i++) {
            Mat pt1 = new Mat(3, 1, CvType.CV_64FC1), pt2 = new Mat();
            pt1.put(0, 0, corners1Arr[i].x, corners1Arr[i].y, 1 );
 
            Core.gemm(H, pt1, 1, new Mat(), 0, pt2);
            double[] data = pt2.get(2, 0);
            Core.divide(pt2, new Scalar(data[0]), pt2);
 
            double[] data1 =pt2.get(0, 0);
            double[] data2 = pt2.get(1, 0);
            Point end = new Point((int)(img1.cols()+ data1[0]), (int)data2[0]);
            Imgproc.line(img_draw_matches, corners1Arr[i], end, RandomColor(), 2);
        }
 
        HighGui.imshow("Draw matches", img_draw_matches);
        HighGui.waitKey(0);

To check the correctness of the calculation, the matching lines are displayed:

Demo 3: Homography from the camera displacement

The homography relates the transformation between two planes and it is possible to retrieve the corresponding camera displacement that allows to go from the first to the second plane view (see [181] for more information). Before going into the details that allow to compute the homography from the camera displacement, some recalls about camera pose and homogeneous transformation.

The function cv::solvePnP allows to compute the camera pose from the correspondences 3D object points (points expressed in the object frame) and the projected 2D image points (object points viewed in the image). The intrinsic parameters and the distortion coefficients are required (see the camera calibration process).

\[ \begin{align*} s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \\ &= \mathbf{K} \hspace{0.2em} ^{c}\mathbf{M}_o \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \end{align*} \]

\( \mathbf{K} \) is the intrinsic matrix and \( ^{c}\mathbf{M}_o \) is the camera pose. The output of cv::solvePnP is exactly this: rvec is the Rodrigues rotation vector and tvec the translation vector.

\( ^{c}\mathbf{M}_o \) can be represented in a homogeneous form and allows to transform a point expressed in the object frame into the camera frame:

\[ \begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\mathbf{M}_o \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} ^{c}\mathbf{R}_o & ^{c}\mathbf{t}_o \\ 0_{1\times3} & 1 \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \end{align*} \]

Transform a point expressed in one frame to another frame can be easily done with matrix multiplication:

• \( ^{c_1}\mathbf{M}_o \) is the camera pose for the camera 1
• \( ^{c_2}\mathbf{M}_o \) is the camera pose for the camera 2

To transform a 3D point expressed in the camera 1 frame to the camera 2 frame:

\[ ^{c_2}\mathbf{M}_{c_1} = \hspace{0.2em} ^{c_2}\mathbf{M}_{o} \cdot \hspace{0.1em} ^{o}\mathbf{M}_{c_1} = \hspace{0.2em} ^{c_2}\mathbf{M}_{o} \cdot \hspace{0.1em} \left( ^{c_1}\mathbf{M}_{o} \right )^{-1} = \begin{bmatrix} ^{c_2}\mathbf{R}_{o} & ^{c_2}\mathbf{t}_{o} \\ 0_{3 \times 1} & 1 \end{bmatrix} \cdot \begin{bmatrix} ^{c_1}\mathbf{R}_{o}^T & - \hspace{0.2em} ^{c_1}\mathbf{R}_{o}^T \cdot \hspace{0.2em} ^{c_1}\mathbf{t}_{o} \\ 0_{1 \times 3} & 1 \end{bmatrix} \]

In this example, we will compute the camera displacement between two camera poses with respect to the chessboard object. The first step consists to compute the camera poses for the two images:

    vector<Point2f> corners1, corners2;
    bool found1 = findChessboardCorners(img1, patternSize, corners1);
    bool found2 = findChessboardCorners(img2, patternSize, corners2);
 
    if (!found1 || !found2)
    {
        cout << "Error, cannot find the chessboard corners in both images." << endl;
        return;
    }
 
    vector<Point3f> objectPoints;
    calcChessboardCorners(patternSize, squareSize, objectPoints);
 
    FileStorage fs( samples::findFile( intrinsicsPath ), FileStorage::READ);
    Mat cameraMatrix, distCoeffs;
    fs["camera_matrix"] >> cameraMatrix;
    fs["distortion_coefficients"] >> distCoeffs;
 
    Mat rvec1, tvec1;
    solvePnP(objectPoints, corners1, cameraMatrix, distCoeffs, rvec1, tvec1);
    Mat rvec2, tvec2;
    solvePnP(objectPoints, corners2, cameraMatrix, distCoeffs, rvec2, tvec2);

The camera displacement can be computed from the camera poses using the formulas above:

void computeC2MC1(const Mat &R1, const Mat &tvec1, const Mat &R2, const Mat &tvec2,
                  Mat &R_1to2, Mat &tvec_1to2)
{
    //c2Mc1 = c2Mo * oMc1 = c2Mo * c1Mo.inv()
    R_1to2 = R2 * R1.t();
    tvec_1to2 = R2 * (-R1.t()*tvec1) + tvec2;
}

The homography related to a specific plane computed from the camera displacement is:

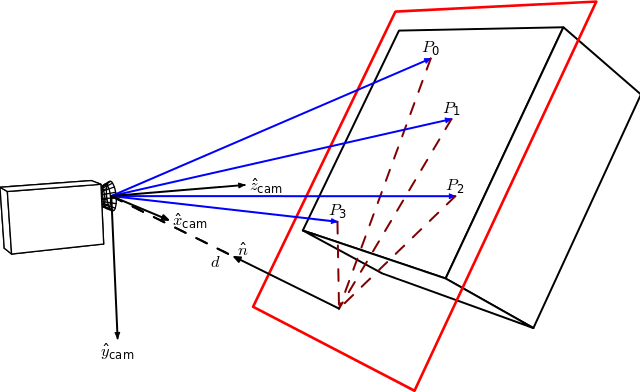
By Homography-transl.svg: Per Rosengren derivative work: Appoose (Homography-transl.svg) [CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons

On this figure, n is the normal vector of the plane and d the distance between the camera frame and the plane along the plane normal. The equation to compute the homography from the camera displacement is:

\[ ^{2}\mathbf{H}_{1} = \hspace{0.2em} ^{2}\mathbf{R}_{1} - \hspace{0.1em} \frac{^{2}\mathbf{t}_{1} \cdot \hspace{0.1em} ^{1}\mathbf{n}^\top}{^1d} \]

Where \( ^{2}\mathbf{H}_{1} \) is the homography matrix that maps the points in the first camera frame to the corresponding points in the second camera frame, \( ^{2}\mathbf{R}_{1} = \hspace{0.2em} ^{c_2}\mathbf{R}_{o} \cdot \hspace{0.1em} ^{c_1}\mathbf{R}_{o}^{\top} \) is the rotation matrix that represents the rotation between the two camera frames and \( ^{2}\mathbf{t}_{1} = \hspace{0.2em} ^{c_2}\mathbf{R}_{o} \cdot \left( - \hspace{0.1em} ^{c_1}\mathbf{R}_{o}^{\top} \cdot \hspace{0.1em} ^{c_1}\mathbf{t}_{o} \right ) + \hspace{0.1em} ^{c_2}\mathbf{t}_{o} \) the translation vector between the two camera frames.

Here the normal vector n is the plane normal expressed in the camera frame 1 and can be computed as the cross product of 2 vectors (using 3 non collinear points that lie on the plane) or in our case directly with:

    Mat normal = (Mat_<double>(3,1) << 0, 0, 1);
    Mat normal1 = R1*normal;

The distance d can be computed as the dot product between the plane normal and a point on the plane or by computing the plane equation and using the D coefficient:

    Mat origin(3, 1, CV_64F, Scalar(0));
    Mat origin1 = R1*origin + tvec1;
    double d_inv1 = 1.0 / normal1.dot(origin1);

The projective homography matrix \( \textbf{G} \) can be computed from the Euclidean homography \( \textbf{H} \) using the intrinsic matrix \( \textbf{K} \) (see [181]), here assuming the same camera between the two plane views:

\[ \textbf{G} = \gamma \textbf{K} \textbf{H} \textbf{K}^{-1} \]

Mat computeHomography(const Mat &R_1to2, const Mat &tvec_1to2, const double d_inv, const Mat &normal)
{
    Mat homography = R_1to2 + d_inv * tvec_1to2*normal.t();
    return homography;
}

In our case, the Z-axis of the chessboard goes inside the object whereas in the homography figure it goes outside. This is just a matter of sign:

\[ ^{2}\mathbf{H}_{1} = \hspace{0.2em} ^{2}\mathbf{R}_{1} + \hspace{0.1em} \frac{^{2}\mathbf{t}_{1} \cdot \hspace{0.1em} ^{1}\mathbf{n}^\top}{^1d} \]

    Mat homography_euclidean = computeHomography(R_1to2, t_1to2, d_inv1, normal1);
    Mat homography = cameraMatrix * homography_euclidean * cameraMatrix.inv();
 
    homography /= homography.at<double>(2,2);
    homography_euclidean /= homography_euclidean.at<double>(2,2);

We will now compare the projective homography computed from the camera displacement with the one estimated with cv::findHomography

findHomography H:
[0.32903393332201, -1.244138808862929, 536.4769088231476;
 0.6969763913334046, -0.08935909072571542, -80.34068504082403;
 0.00040511729592961, -0.001079740100565013, 0.9999999999999999]
 
homography from camera displacement:
[0.4160569997384721, -1.306889006892538, 553.7055461075881;
 0.7917584252773352, -0.06341244158456338, -108.2770029401219;
 0.0005926357240956578, -0.001020651672127799, 1]

The homography matrices are similar. If we compare the image 1 warped using both homography matrices:

Left: image warped using the estimated homography. Right: using the homography computed from the camera displacement.

Visually, it is hard to distinguish a difference between the result image from the homography computed from the camera displacement and the one estimated with cv::findHomography function.

Exercise

This demo shows you how to compute the homography transformation from two camera poses. Try to perform the same operations, but by computing N inter homography this time. Instead of computing one homography to directly warp the source image to the desired camera viewpoint, perform N warping operations to see the different transformations operating.

You should get something similar to the following:

The first three images show the source image warped at three different interpolated camera viewpoints. The 4th image shows the "error image" between the warped source image at the final camera viewpoint and the desired image.

Demo 4: Decompose the homography matrix

OpenCV 3 contains the function cv::decomposeHomographyMat which allows to decompose the homography matrix to a set of rotations, translations and plane normals. First we will decompose the homography matrix computed from the camera displacement:

    Mat homography_euclidean = computeHomography(R_1to2, t_1to2, d_inv1, normal1);
    Mat homography = cameraMatrix * homography_euclidean * cameraMatrix.inv();
 
    homography /= homography.at<double>(2,2);
    homography_euclidean /= homography_euclidean.at<double>(2,2);

The results of cv::decomposeHomographyMat are:

    vector<Mat> Rs_decomp, ts_decomp, normals_decomp;
    int solutions = decomposeHomographyMat(homography, cameraMatrix, Rs_decomp, ts_decomp, normals_decomp);
    cout << "Decompose homography matrix computed from the camera displacement:" << endl << endl;
    for (int i = 0; i < solutions; i++)
    {
      double factor_d1 = 1.0 / d_inv1;
      Mat rvec_decomp;
      Rodrigues(Rs_decomp[i], rvec_decomp);
      cout << "Solution " << i << ":" << endl;
      cout << "rvec from homography decomposition: " << rvec_decomp.t() << endl;
      cout << "rvec from camera displacement: " << rvec_1to2.t() << endl;
      cout << "tvec from homography decomposition: " << ts_decomp[i].t() << " and scaled by d: " << factor_d1 * ts_decomp[i].t() << endl;
      cout << "tvec from camera displacement: " << t_1to2.t() << endl;
      cout << "plane normal from homography decomposition: " << normals_decomp[i].t() << endl;
      cout << "plane normal at camera 1 pose: " << normal1.t() << endl << endl;
    }

Solution 0:
rvec from homography decomposition: [-0.0919829920641369, -0.5372581036567992, 1.310868863540717]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [-0.7747961019053186, -0.02751124463434032, -0.6791980037590677] and scaled by d: [-0.1578091561210742, -0.005603443652993778, -0.1383378976078466]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [-0.1973513139420648, 0.6283451996579074, -0.7524857267431757]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
Solution 1:
rvec from homography decomposition: [-0.0919829920641369, -0.5372581036567992, 1.310868863540717]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [0.7747961019053186, 0.02751124463434032, 0.6791980037590677] and scaled by d: [0.1578091561210742, 0.005603443652993778, 0.1383378976078466]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [0.1973513139420648, -0.6283451996579074, 0.7524857267431757]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
Solution 2:
rvec from homography decomposition: [0.1053487907109967, -0.1561929144786397, 1.401356552358475]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [-0.4666552552894618, 0.1050032934770042, -0.913007654671646] and scaled by d: [-0.0950475510338766, 0.02138689274867372, -0.1859598508065552]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [-0.3131715472900788, 0.8421206145721947, -0.4390403768225507]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
Solution 3:
rvec from homography decomposition: [0.1053487907109967, -0.1561929144786397, 1.401356552358475]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [0.4666552552894618, -0.1050032934770042, 0.913007654671646] and scaled by d: [0.0950475510338766, -0.02138689274867372, 0.1859598508065552]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [0.3131715472900788, -0.8421206145721947, 0.4390403768225507]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]

The result of the decomposition of the homography matrix can only be recovered up to a scale factor that corresponds in fact to the distance d as the normal is unit length. As you can see, there is one solution that matches almost perfectly with the computed camera displacement. As stated in the documentation:

At least two of the solutions may further be invalidated if point correspondences are available by applying positive depth constraint (all points must be in front of the camera).

As the result of the decomposition is a camera displacement, if we have the initial camera pose \( ^{c_1}\mathbf{M}_{o} \), we can compute the current camera pose \( ^{c_2}\mathbf{M}_{o} = \hspace{0.2em} ^{c_2}\mathbf{M}_{c_1} \cdot \hspace{0.1em} ^{c_1}\mathbf{M}_{o} \) and test if the 3D object points that belong to the plane are projected in front of the camera or not. Another solution could be to retain the solution with the closest normal if we know the plane normal expressed at the camera 1 pose.

The same thing but with the homography matrix estimated with cv::findHomography

Solution 0:
rvec from homography decomposition: [0.1552207729599141, -0.152132696119647, 1.323678695078694]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [-0.4482361704818117, 0.02485247635491922, -1.034409687207331] and scaled by d: [-0.09129598307571339, 0.005061910238634657, -0.2106868109173855]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [-0.1384902722707529, 0.9063331452766947, -0.3992250922214516]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
Solution 1:
rvec from homography decomposition: [0.1552207729599141, -0.152132696119647, 1.323678695078694]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [0.4482361704818117, -0.02485247635491922, 1.034409687207331] and scaled by d: [0.09129598307571339, -0.005061910238634657, 0.2106868109173855]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [0.1384902722707529, -0.9063331452766947, 0.3992250922214516]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
Solution 2:
rvec from homography decomposition: [-0.2886605671759886, -0.521049903923871, 1.381242030882511]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [-0.8705961357284295, 0.1353018038908477, -0.7037702049789747] and scaled by d: [-0.177321544550518, 0.02755804196893467, -0.1433427218822783]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [-0.2284582117722427, 0.6009247303964522, -0.7659610393954643]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
Solution 3:
rvec from homography decomposition: [-0.2886605671759886, -0.521049903923871, 1.381242030882511]
rvec from camera displacement: [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
tvec from homography decomposition: [0.8705961357284295, -0.1353018038908477, 0.7037702049789747] and scaled by d: [0.177321544550518, -0.02755804196893467, 0.1433427218822783]
tvec from camera displacement: [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
plane normal from homography decomposition: [0.2284582117722427, -0.6009247303964522, 0.7659610393954643]
plane normal at camera 1 pose: [0.1973513139420654, -0.6283451996579068, 0.752485726743176]

Again, there is also a solution that matches with the computed camera displacement.

Demo 5: Basic panorama stitching from a rotating camera

Note

This example is made to illustrate the concept of image stitching based on a pure rotational motion of the camera and should not be used to stitch panorama images. The stitching module provides a complete pipeline to stitch images.

The homography transformation applies only for planar structure. But in the case of a rotating camera (pure rotation around the camera axis of projection, no translation), an arbitrary world can be considered (see previously).

The homography can then be computed using the rotation transformation and the camera intrinsic parameters as (see for instance 10):

\[ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = \bf{K} \hspace{0.1em} \bf{R} \hspace{0.1em} \bf{K}^{-1} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

To illustrate, we used Blender, a free and open-source 3D computer graphics software, to generate two camera views with only a rotation transformation between each other. More information about how to retrieve the camera intrinsic parameters and the 3x4 extrinsic matrix with respect to the world can be found in 11 (an additional transformation is needed to get the transformation between the camera and the object frames) with Blender.

The figure below shows the two generated views of the Suzanne model, with only a rotation transformation:

With the known associated camera poses and the intrinsic parameters, the relative rotation between the two views can be computed:

C++

    Mat R1 = c1Mo(Range(0,3), Range(0,3));
    Mat R2 = c2Mo(Range(0,3), Range(0,3));

Python

    R1 = c1Mo[0:3, 0:3]
    R2 = c2Mo[0:3, 0:3]

Java

        Range rowRange = new Range(0,3);
        Range colRange = new Range(0,3);

C++

    //c1Mo * oMc2
    Mat R_2to1 = R1*R2.t();

Python

    R2 = R2.transpose()
    R_2to1 = np.dot(R1,R2)

Java

        //c1Mo * oMc2
        Mat R1 = new  Mat(c1Mo, rowRange, colRange);
        Mat R2 = new Mat(c2Mo, rowRange, colRange);
        Mat R_2to1 = new Mat();
        Core.gemm(R1, R2.t(), 1, new Mat(), 0, R_2to1 );

Here, the second image will be stitched with respect to the first image. The homography can be calculated using the formula above:

C++

    Mat H = cameraMatrix * R_2to1 * cameraMatrix.inv();
    H /= H.at<double>(2,2);
    cout << "H:\n" << H << endl;

Python

    H = cameraMatrix.dot(R_2to1).dot(np.linalg.inv(cameraMatrix))
    H = H / H[2][2]

Java

        Mat tmp = new Mat(), H = new Mat();
        Core.gemm(cameraMatrix, R_2to1, 1, new Mat(), 0, tmp);
        Core.gemm(tmp, cameraMatrix.inv(), 1, new Mat(), 0, H);
        Scalar s = new Scalar(H.get(2, 2)[0]);
        Core.divide(H, s, H);
        System.out.println(H.dump());

The stitching is made simply with:

C++

    Mat img_stitch;
    warpPerspective(img2, img_stitch, H, Size(img2.cols*2, img2.rows));
    Mat half = img_stitch(Rect(0, 0, img1.cols, img1.rows));
    img1.copyTo(half);

Python

    img_stitch = cv.warpPerspective(img2, H, (img2.shape[1]*2, img2.shape[0]))
    img_stitch[0:img1.shape[0], 0:img1.shape[1]] = img1

Java

        Mat img_stitch = new Mat();
        Imgproc.warpPerspective(img2, img_stitch, H, new Size(img2.cols()*2, img2.rows()) );
        Mat half = new Mat();
        half =  new Mat(img_stitch, new Rect(0, 0, img1.cols(), img1.rows()));
        img1.copyTo(half);

The resulting image is:

Additional references

• 1. Lecture 16: Planar Homographies, Robert Collins
• 2. 2D projective transformations (homographies), Christiano Gava, Gabriele Bleser
• 3. Computer Vision: Algorithms and Applications, Richard Szeliski
• 4. Step by Step Camera Pose Estimation for Visual Tracking and Planar Markers
• 5. Pose from homography estimation
• 6. Polar Decomposition (in Continuum Mechanics)
• 7. Chapter 3 - 3.1.2 From matrices to rotations - Theorem 3.1 (Least-squares estimation of a rotation from a matrix K)
• 8. A Personal Interview with the Singular Value Decomposition, Matan Gavish
• 9. Kabsch algorithm, Computation of the optimal rotation matrix
• 10. Homography, Dr. Gerhard Roth
• 11. 3x4 camera matrix from blender camera