 |
OpenCV 5.0.0-pre
Open Source Computer Vision
|
 |
OpenCV 5.0.0-pre
Open Source Computer Vision
|
Topics | |
| Fisheye camera model | |
The functions in this section use a so-called pinhole camera model. The view of a scene is obtained by projecting a scene's 3D point \(P_w\) into the image plane using a perspective transformation which forms the corresponding pixel \(p\). Both \(P_w\) and \(p\) are represented in homogeneous coordinates, i.e. as 3D and 2D homogeneous vector respectively. You will find a brief introduction to projective geometry, homogeneous vectors and homogeneous transformations at the end of this section's introduction. For more succinct notation, we often drop the 'homogeneous' and say vector instead of homogeneous vector.
The distortion-free projective transformation given by a pinhole camera model is shown below.
\[s \; p = A \begin{bmatrix} R|t \end{bmatrix} P_w,\]
where \(P_w\) is a 3D point expressed with respect to the world coordinate system, \(p\) is a 2D pixel in the image plane, \(A\) is the camera intrinsic matrix, \(R\) and \(t\) are the rotation and translation that describe the change of coordinates from world to camera coordinate systems (or camera frame) and \(s\) is the projective transformation's arbitrary scaling and not part of the camera model.
The camera intrinsic matrix \(A\) (notation used as in [323] and also generally notated as \(K\)) projects 3D points given in the camera coordinate system to 2D pixel coordinates, i.e.
\[p = A P_c.\]
The camera intrinsic matrix \(A\) is composed of the focal lengths \(f_x\) and \(f_y\), which are expressed in pixel units, and the principal point \((c_x, c_y)\), that is usually close to the image center:
\[A = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1},\]
and thus
\[s \vecthree{u}{v}{1} = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1} \vecthree{X_c}{Y_c}{Z_c}.\]
The matrix of intrinsic parameters does not depend on the scene viewed. So, once estimated, it can be re-used as long as the focal length is fixed (in case of a zoom lens). Thus, if an image from the camera is scaled by a factor, all of these parameters need to be scaled (multiplied/divided, respectively) by the same factor.
The joint rotation-translation matrix \([R|t]\) is the matrix product of a projective transformation and a homogeneous transformation. The 3-by-4 projective transformation maps 3D points represented in camera coordinates to 2D points in the image plane and represented in normalized camera coordinates \(x' = X_c / Z_c\) and \(y' = Y_c / Z_c\):
\[Z_c \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix}.\]
The homogeneous transformation is encoded by the extrinsic parameters \(R\) and \(t\) and represents the change of basis from world coordinate system \(w\) to the camera coordinate sytem \(c\). Thus, given the representation of the point \(P\) in world coordinates, \(P_w\), we obtain \(P\)'s representation in the camera coordinate system, \(P_c\), by
\[P_c = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} P_w,\]
This homogeneous transformation is composed out of \(R\), a 3-by-3 rotation matrix, and \(t\), a 3-by-1 translation vector:
\[\begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}, \]
and therefore
\[\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}.\]
Combining the projective transformation and the homogeneous transformation, we obtain the projective transformation that maps 3D points in world coordinates into 2D points in the image plane and in normalized camera coordinates:
\[Z_c \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R|t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix},\]
with \(x' = X_c / Z_c\) and \(y' = Y_c / Z_c\). Putting the equations for instrincs and extrinsics together, we can write out \(s \; p = A \begin{bmatrix} R|t \end{bmatrix} P_w\) as
\[s \vecthree{u}{v}{1} = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}.\]
If \(Z_c \ne 0\), the transformation above is equivalent to the following,
\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x X_c/Z_c + c_x \\ f_y Y_c/Z_c + c_y \end{bmatrix}\]
with
\[\vecthree{X_c}{Y_c}{Z_c} = \begin{bmatrix} R|t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}.\]
The following figure illustrates the pinhole camera model.

Real lenses usually have some distortion, mostly radial distortion, and slight tangential distortion. So, the above model is extended as:
\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x x'' + c_x \\ f_y y'' + c_y \end{bmatrix}\]
where
\[\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} x' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + 2 p_1 x' y' + p_2(r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4 \\ y' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \\ \end{bmatrix}\]
with
\[r^2 = x'^2 + y'^2\]
and
\[\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} X_c/Z_c \\ Y_c/Z_c \end{bmatrix},\]
if \(Z_c \ne 0\).
The distortion parameters are the radial coefficients \(k_1\), \(k_2\), \(k_3\), \(k_4\), \(k_5\), and \(k_6\) , \(p_1\) and \(p_2\) are the tangential distortion coefficients, and \(s_1\), \(s_2\), \(s_3\), and \(s_4\), are the thin prism distortion coefficients. Higher-order coefficients are not considered in OpenCV.
The next figures show two common types of radial distortion: barrel distortion ( \( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6 \) monotonically decreasing) and pincushion distortion ( \( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6 \) monotonically increasing). Radial distortion is always monotonic for real lenses, and if the estimator produces a non-monotonic result, this should be considered a calibration failure. More generally, radial distortion must be monotonic and the distortion function must be bijective. A failed estimation result may look deceptively good near the image center but will work poorly in e.g. AR/SFM applications. The optimization method used in OpenCV camera calibration does not include these constraints as the framework does not support the required integer programming and polynomial inequalities. See issue #15992 for additional information.


In some cases, the image sensor may be tilted in order to focus an oblique plane in front of the camera (Scheimpflug principle). This can be useful for particle image velocimetry (PIV) or triangulation with a laser fan. The tilt causes a perspective distortion of \(x''\) and \(y''\). This distortion can be modeled in the following way, see e.g. [175].
\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x x''' + c_x \\ f_y y''' + c_y \end{bmatrix},\]
where
\[s\vecthree{x'''}{y'''}{1} = \vecthreethree{R_{33}(\tau_x, \tau_y)}{0}{-R_{13}(\tau_x, \tau_y)} {0}{R_{33}(\tau_x, \tau_y)}{-R_{23}(\tau_x, \tau_y)} {0}{0}{1} R(\tau_x, \tau_y) \vecthree{x''}{y''}{1}\]
and the matrix \(R(\tau_x, \tau_y)\) is defined by two rotations with angular parameter \(\tau_x\) and \(\tau_y\), respectively,
\[ R(\tau_x, \tau_y) = \vecthreethree{\cos(\tau_y)}{0}{-\sin(\tau_y)}{0}{1}{0}{\sin(\tau_y)}{0}{\cos(\tau_y)} \vecthreethree{1}{0}{0}{0}{\cos(\tau_x)}{\sin(\tau_x)}{0}{-\sin(\tau_x)}{\cos(\tau_x)} = \vecthreethree{\cos(\tau_y)}{\sin(\tau_y)\sin(\tau_x)}{-\sin(\tau_y)\cos(\tau_x)} {0}{\cos(\tau_x)}{\sin(\tau_x)} {\sin(\tau_y)}{-\cos(\tau_y)\sin(\tau_x)}{\cos(\tau_y)\cos(\tau_x)}. \]
In the functions below the coefficients are passed or returned as
\[(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\]
vector. That is, if the vector contains four elements, it means that \(k_3=0\) . The distortion coefficients do not depend on the scene viewed. Thus, they also belong to the intrinsic camera parameters. And they remain the same regardless of the captured image resolution. If, for example, a camera has been calibrated on images of 320 x 240 resolution, absolutely the same distortion coefficients can be used for 640 x 480 images from the same camera while \(f_x\), \(f_y\), \(c_x\), and \(c_y\) need to be scaled appropriately.
The functions below use the above model to do the following:
Homogeneous Coordinates
Homogeneous Coordinates are a system of coordinates that are used in projective geometry. Their use allows to represent points at infinity by finite coordinates and simplifies formulas when compared to the cartesian counterparts, e.g. they have the advantage that affine transformations can be expressed as linear homogeneous transformation.
One obtains the homogeneous vector \(P_h\) by appending a 1 along an n-dimensional cartesian vector \(P\) e.g. for a 3D cartesian vector the mapping \(P \rightarrow P_h\) is:
\[\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \rightarrow \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}.\]
For the inverse mapping \(P_h \rightarrow P\), one divides all elements of the homogeneous vector by its last element, e.g. for a 3D homogeneous vector one gets its 2D cartesian counterpart by:
\[\begin{bmatrix} X \\ Y \\ W \end{bmatrix} \rightarrow \begin{bmatrix} X / W \\ Y / W \end{bmatrix},\]
if \(W \ne 0\).
Due to this mapping, all multiples \(k P_h\), for \(k \ne 0\), of a homogeneous point represent the same point \(P_h\). An intuitive understanding of this property is that under a projective transformation, all multiples of \(P_h\) are mapped to the same point. This is the physical observation one does for pinhole cameras, as all points along a ray through the camera's pinhole are projected to the same image point, e.g. all points along the red ray in the image of the pinhole camera model above would be mapped to the same image coordinate. This property is also the source for the scale ambiguity s in the equation of the pinhole camera model.
As mentioned, by using homogeneous coordinates we can express any change of basis parameterized by \(R\) and \(t\) as a linear transformation, e.g. for the change of basis from coordinate system 0 to coordinate system 1 becomes:
\[P_1 = R P_0 + t \rightarrow P_{h_1} = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} P_{h_0}.\]
Homogeneous Transformations, Object frame / Camera frame
Change of basis or computing the 3D coordinates from one frame to another frame can be achieved easily using the following notation:
\[ \mathbf{X}_c = \hspace{0.2em} {}^{c}\mathbf{T}_o \hspace{0.2em} \mathbf{X}_o \]
\[ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} = \begin{bmatrix} {}^{c}\mathbf{R}_o & {}^{c}\mathbf{t}_o \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \]
For a 3D points ( \( \mathbf{X}_o \)) expressed in the object frame, the homogeneous transformation matrix \( {}^{c}\mathbf{T}_o \) allows computing the corresponding coordinate ( \( \mathbf{X}_c \)) in the camera frame. This transformation matrix is composed of a 3x3 rotation matrix \( {}^{c}\mathbf{R}_o \) and a 3x1 translation vector \( {}^{c}\mathbf{t}_o \). The 3x1 translation vector \( {}^{c}\mathbf{t}_o \) is the position of the object frame in the camera frame and the 3x3 rotation matrix \( {}^{c}\mathbf{R}_o \) the orientation of the object frame in the camera frame. With this simple notation, it is easy to chain the transformations. For instance, to compute the 3D coordinates of a point expressed in the object frame in the world frame can be done with:
\[ \mathbf{X}_w = \hspace{0.2em} {}^{w}\mathbf{T}_c \hspace{0.2em} {}^{c}\mathbf{T}_o \hspace{0.2em} \mathbf{X}_o = {}^{w}\mathbf{T}_o \hspace{0.2em} \mathbf{X}_o \]
Similarly, computing the inverse transformation can be done with:
\[ \mathbf{X}_o = \hspace{0.2em} {}^{o}\mathbf{T}_c \hspace{0.2em} \mathbf{X}_c = \left( {}^{c}\mathbf{T}_o \right)^{-1} \hspace{0.2em} \mathbf{X}_c \]
The inverse of an homogeneous transformation matrix is then:
\[ {}^{o}\mathbf{T}_c = \left( {}^{c}\mathbf{T}_o \right)^{-1} = \begin{bmatrix} {}^{c}\mathbf{R}^{\top}_o & - \hspace{0.2em} {}^{c}\mathbf{R}^{\top}_o \hspace{0.2em} {}^{c}\mathbf{t}_o \\ 0_{1 \times 3} & 1 \end{bmatrix} \]
One can note that the inverse of a 3x3 rotation matrix is directly its matrix transpose. 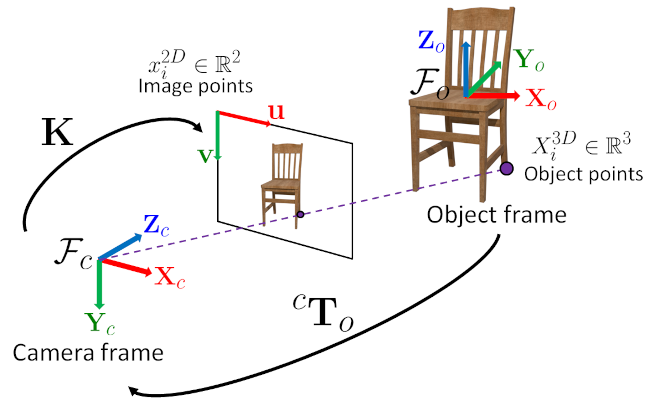
This figure summarizes the whole process. The object pose returned for instance by the solvePnP function or pose from fiducial marker detection is this \( {}^{c}\mathbf{T}_o \) transformation. The camera intrinsic matrix \( \mathbf{K} \) allows projecting the 3D point expressed in the camera frame onto the image plane assuming a perspective projection model (pinhole camera model). Image coordinates extracted from classical image processing functions assume a (u,v) top-left coordinates frame.
\[ f_x = \frac{f_{\text{mm}}}{\text{pixel_size_in_mm}} = \frac{f_{\text{mm}}}{\text{sensor_size_in_mm} / \text{nb_pixels}} \]
In a same way, the physical focal length can be deduced from the angular field of view:\[ f_{\text{mm}} = \frac{\text{sensor_size_in_mm}}{2 \times \tan{\frac{\text{fov}}{2}}} \]
This latter conversion can be useful when using a rendering software to mimic a physical camera device. Additional references, notes
Namespaces | |
| namespace | cv::fisheye |
| The methods in this namespace use a so-called fisheye camera model. | |
Classes | |
| struct | cv::CirclesGridFinderParameters |
Macros | |
| #define | CALIB_NINTRINSIC 18 |
| Maximal size of camera internal parameters (initrinsics) vector. | |
Typedefs | |
| typedef CirclesGridFinderParameters | cv::CirclesGridFinderParameters2 |
Functions | |
| cv::CirclesGridFinderParameters::CirclesGridFinderParameters () | |
| double | cv::calibrateCamera (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON)) |
| double | cv::calibrateCamera (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray stdDeviationsIntrinsics, OutputArray stdDeviationsExtrinsics, OutputArray perViewErrors, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON)) |
| Finds the camera intrinsic and extrinsic parameters from several views of a calibration pattern. | |
| double | cv::calibrateCameraRO (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, int iFixedPoint, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray newObjPoints, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON)) |
| double | cv::calibrateCameraRO (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, int iFixedPoint, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray newObjPoints, OutputArray stdDeviationsIntrinsics, OutputArray stdDeviationsExtrinsics, OutputArray stdDeviationsObjPoints, OutputArray perViewErrors, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON)) |
| Finds the camera intrinsic and extrinsic parameters from several views of a calibration pattern. | |
| void | cv::calibrateHandEye (InputArrayOfArrays R_gripper2base, InputArrayOfArrays t_gripper2base, InputArrayOfArrays R_target2cam, InputArrayOfArrays t_target2cam, OutputArray R_cam2gripper, OutputArray t_cam2gripper, HandEyeCalibrationMethod method=CALIB_HAND_EYE_TSAI) |
| Computes Hand-Eye calibration: \(_{}^{g}\textrm{T}_c\). | |
| double | cv::calibrateMultiview (InputArrayOfArrays objPoints, const std::vector< std::vector< Mat > > &imagePoints, const std::vector< cv::Size > &imageSize, InputArray detectionMask, InputArray models, InputOutputArrayOfArrays Ks, InputOutputArrayOfArrays distortions, InputOutputArrayOfArrays Rs, InputOutputArrayOfArrays Ts, InputArray flagsForIntrinsics=noArray(), int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON)) |
| This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. | |
| double | cv::calibrateMultiview (InputArrayOfArrays objPoints, const std::vector< std::vector< Mat > > &imagePoints, const std::vector< cv::Size > &imageSize, InputArray detectionMask, InputArray models, InputOutputArrayOfArrays Ks, InputOutputArrayOfArrays distortions, InputOutputArrayOfArrays Rs, InputOutputArrayOfArrays Ts, OutputArray initializationPairs, OutputArrayOfArrays rvecs0, OutputArrayOfArrays tvecs0, OutputArray perFrameErrors, InputArray flagsForIntrinsics=noArray(), int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON)) |
| Estimates intrinsics and extrinsics (camera pose) for multi-camera system a.k.a multiview calibration. | |
| void | cv::calibrateRobotWorldHandEye (InputArrayOfArrays R_world2cam, InputArrayOfArrays t_world2cam, InputArrayOfArrays R_base2gripper, InputArrayOfArrays t_base2gripper, OutputArray R_base2world, OutputArray t_base2world, OutputArray R_gripper2cam, OutputArray t_gripper2cam, RobotWorldHandEyeCalibrationMethod method=CALIB_ROBOT_WORLD_HAND_EYE_SHAH) |
| Computes Robot-World/Hand-Eye calibration: \(_{}^{w}\textrm{T}_b\) and \(_{}^{c}\textrm{T}_g\). | |
| void | cv::calibrationMatrixValues (InputArray cameraMatrix, Size imageSize, double apertureWidth, double apertureHeight, double &fovx, double &fovy, double &focalLength, Point2d &principalPoint, double &aspectRatio) |
| Computes useful camera characteristics from the camera intrinsic matrix. | |
| bool | cv::checkChessboard (InputArray img, Size size) |
| void | cv::drawChessboardCorners (InputOutputArray image, Size patternSize, InputArray corners, bool patternWasFound) |
| Renders the detected chessboard corners. | |
| Scalar | cv::estimateChessboardSharpness (InputArray image, Size patternSize, InputArray corners, float rise_distance=0.8F, bool vertical=false, OutputArray sharpness=noArray()) |
| Estimates the sharpness of a detected chessboard. | |
| bool | cv::find4QuadCornerSubpix (InputArray img, InputOutputArray corners, Size region_size) |
| finds subpixel-accurate positions of the chessboard corners | |
| bool | cv::findChessboardCorners (InputArray image, Size patternSize, OutputArray corners, int flags=CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE) |
| Finds the positions of internal corners of the chessboard. | |
| bool | cv::findChessboardCornersSB (InputArray image, Size patternSize, OutputArray corners, int flags, OutputArray meta) |
| Finds the positions of internal corners of the chessboard using a sector based approach. | |
| bool | cv::findChessboardCornersSB (InputArray image, Size patternSize, OutputArray corners, int flags=0) |
| bool | cv::findCirclesGrid (InputArray image, Size patternSize, OutputArray centers, int flags, const Ptr< FeatureDetector > &blobDetector, const CirclesGridFinderParameters ¶meters) |
| Finds centers in the grid of circles. | |
| bool | cv::findCirclesGrid (InputArray image, Size patternSize, OutputArray centers, int flags=CALIB_CB_SYMMETRIC_GRID, const Ptr< FeatureDetector > &blobDetector=SimpleBlobDetector::create()) |
| Mat | cv::initCameraMatrix2D (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, double aspectRatio=1.0) |
| Finds an initial camera intrinsic matrix from 3D-2D point correspondences. | |
| double | cv::registerCameras (InputArrayOfArrays objectPoints1, InputArrayOfArrays objectPoints2, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputArray cameraMatrix1, InputArray distCoeffs1, CameraModel cameraModel1, InputArray cameraMatrix2, InputArray distCoeffs2, CameraModel cameraModel2, InputOutputArray R, InputOutputArray T, OutputArray E, OutputArray F, OutputArray perViewErrors, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6)) |
| This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. | |
| double | cv::registerCameras (InputArrayOfArrays objectPoints1, InputArrayOfArrays objectPoints2, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputArray cameraMatrix1, InputArray distCoeffs1, CameraModel cameraModel1, InputArray cameraMatrix2, InputArray distCoeffs2, CameraModel cameraModel2, InputOutputArray R, InputOutputArray T, OutputArray E, OutputArray F, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray perViewErrors, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6)) |
| Calibrates a camera pair set up. This function finds the extrinsic parameters between the two cameras. | |
| double | cv::stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, Size imageSize, InputOutputArray R, InputOutputArray T, OutputArray E, OutputArray F, OutputArray perViewErrors, int flags=CALIB_FIX_INTRINSIC, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6)) |
| This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. | |
| double | cv::stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, Size imageSize, InputOutputArray R, InputOutputArray T, OutputArray E, OutputArray F, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray perViewErrors, int flags=CALIB_FIX_INTRINSIC, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6)) |
| Calibrates a stereo camera set up. This function finds the intrinsic parameters for each of the two cameras and the extrinsic parameters between the two cameras. | |
| double | cv::stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, Size imageSize, OutputArray R, OutputArray T, OutputArray E, OutputArray F, int flags=CALIB_FIX_INTRINSIC, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6)) |
| This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. | |
| #define CALIB_NINTRINSIC 18 |
#include <opencv2/calib.hpp>
Maximal size of camera internal parameters (initrinsics) vector.
#include <opencv2/calib.hpp>
| anonymous enum |
#include <opencv2/calib.hpp>
| anonymous enum |
#include <opencv2/calib.hpp>
| Enumerator | |
|---|---|
| CALIB_CB_SYMMETRIC_GRID Python: cv.CALIB_CB_SYMMETRIC_GRID | |
| CALIB_CB_ASYMMETRIC_GRID Python: cv.CALIB_CB_ASYMMETRIC_GRID | |
| CALIB_CB_CLUSTERING Python: cv.CALIB_CB_CLUSTERING | |
| anonymous enum |
#include <opencv2/calib.hpp>
| Enumerator | |
|---|---|
| CALIB_USE_INTRINSIC_GUESS Python: cv.CALIB_USE_INTRINSIC_GUESS | Use user provided intrinsics as initial point for optimization. |
| CALIB_FIX_ASPECT_RATIO Python: cv.CALIB_FIX_ASPECT_RATIO | Use with CALIB_USE_INTRINSIC_GUESS. The ratio fx/fy stays the same as in the input cameraMatrix. |
| CALIB_FIX_PRINCIPAL_POINT Python: cv.CALIB_FIX_PRINCIPAL_POINT | The principal point (cx, cy) stays the same as in the input camera matrix. Image center is used as principal point, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_ZERO_TANGENT_DIST Python: cv.CALIB_ZERO_TANGENT_DIST | For pinhole model only. Tangential distortion coefficients \((p_1, p_2)\) are set to zeros and stay zero. |
| CALIB_FIX_FOCAL_LENGTH Python: cv.CALIB_FIX_FOCAL_LENGTH | Use with CALIB_USE_INTRINSIC_GUESS. The focal length (fx, fy) stays the same as in the input cameraMatrix. |
| CALIB_FIX_K1 Python: cv.CALIB_FIX_K1 | The corresponding distortion coefficient is not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_FIX_K2 Python: cv.CALIB_FIX_K2 | The corresponding distortion coefficient is not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_FIX_K3 Python: cv.CALIB_FIX_K3 | The corresponding distortion coefficient is not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_FIX_K4 Python: cv.CALIB_FIX_K4 | The corresponding distortion coefficient is not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_FIX_K5 Python: cv.CALIB_FIX_K5 | For pinhole model only. The corresponding distortion coefficient is not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_FIX_K6 Python: cv.CALIB_FIX_K6 | For pinhole model only. The corresponding distortion coefficient is not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_RATIONAL_MODEL Python: cv.CALIB_RATIONAL_MODEL | For pinhole model only. Use rational distortion model with coefficients k4..k6. |
| CALIB_THIN_PRISM_MODEL Python: cv.CALIB_THIN_PRISM_MODEL | For pinhole model only. Use thin prism distortion model with coefficients s1..s4. |
| CALIB_FIX_S1_S2_S3_S4 Python: cv.CALIB_FIX_S1_S2_S3_S4 | For pinhole model only. The thin prism distortion coefficients are not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_TILTED_MODEL Python: cv.CALIB_TILTED_MODEL | For pinhole model only. Coefficients tauX and tauY are enabled in camera matrix. |
| CALIB_FIX_TAUX_TAUY Python: cv.CALIB_FIX_TAUX_TAUY | For pinhole model only. The tauX and tauY coefficients are not changed during the optimization. 0 value is used, if CALIB_USE_INTRINSIC_GUESS is not set. |
| CALIB_USE_QR Python: cv.CALIB_USE_QR | Use QR instead of SVD decomposition for solving. Faster but potentially less precise. |
| CALIB_FIX_TANGENT_DIST Python: cv.CALIB_FIX_TANGENT_DIST | For pinhole model only. Tangential distortion coefficients (p1,p2) are set to zeros and stay zero. |
| CALIB_FIX_INTRINSIC Python: cv.CALIB_FIX_INTRINSIC | For stereo and milti-camera calibration only. Do not optimize cameras intrinsics. |
| CALIB_SAME_FOCAL_LENGTH Python: cv.CALIB_SAME_FOCAL_LENGTH | For stereo calibration only. Use the same focal length for cameras in pair. |
| CALIB_ZERO_DISPARITY Python: cv.CALIB_ZERO_DISPARITY | Deprecated synonim of STEREO_ZERO_DISPARITY. See stereoRectify. |
| CALIB_USE_LU Python: cv.CALIB_USE_LU | use LU instead of SVD decomposition for solving. much faster but potentially less precise |
| CALIB_USE_EXTRINSIC_GUESS Python: cv.CALIB_USE_EXTRINSIC_GUESS | For stereo and multi-view calibration. Use user provided extrinsics (R, T) as initial point for optimization. |
| CALIB_RECOMPUTE_EXTRINSIC Python: cv.CALIB_RECOMPUTE_EXTRINSIC | For fisheye model only. Recompute board position on each calibration iteration. |
| CALIB_CHECK_COND Python: cv.CALIB_CHECK_COND | For fisheye model only. Check SVD decomposition quality for each frame during extrinsics estimation. |
| CALIB_FIX_SKEW Python: cv.CALIB_FIX_SKEW | For fisheye model only. Skew coefficient (alpha) is set to zero and stay zero. |
| CALIB_STEREO_REGISTRATION Python: cv.CALIB_STEREO_REGISTRATION | For multiview calibration only. Use stereo correspondence approach for initial extrinsics guess. Limitation: all cameras should have the same type. |
| enum cv::CameraModel |
#include <opencv2/calib.hpp>
| Enumerator | |
|---|---|
| CALIB_MODEL_PINHOLE Python: cv.CALIB_MODEL_PINHOLE | Pinhole camera model. |
| CALIB_MODEL_FISHEYE Python: cv.CALIB_MODEL_FISHEYE | Fisheye camera model. |
#include <opencv2/calib.hpp>
| Enumerator | |
|---|---|
| CALIB_HAND_EYE_TSAI Python: cv.CALIB_HAND_EYE_TSAI | A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration [279]. |
| CALIB_HAND_EYE_PARK Python: cv.CALIB_HAND_EYE_PARK | Robot Sensor Calibration: Solving AX = XB on the Euclidean Group [217]. |
| CALIB_HAND_EYE_HORAUD Python: cv.CALIB_HAND_EYE_HORAUD | Hand-eye Calibration [129]. |
| CALIB_HAND_EYE_ANDREFF Python: cv.CALIB_HAND_EYE_ANDREFF | On-line Hand-Eye Calibration [14]. |
| CALIB_HAND_EYE_DANIILIDIS Python: cv.CALIB_HAND_EYE_DANIILIDIS | Hand-Eye Calibration Using Dual Quaternions [68]. |
#include <opencv2/calib.hpp>
| Enumerator | |
|---|---|
| CALIB_ROBOT_WORLD_HAND_EYE_SHAH Python: cv.CALIB_ROBOT_WORLD_HAND_EYE_SHAH | Solving the robot-world/hand-eye calibration problem using the kronecker product [249]. |
| CALIB_ROBOT_WORLD_HAND_EYE_LI Python: cv.CALIB_ROBOT_WORLD_HAND_EYE_LI | Simultaneous robot-world and hand-eye calibration using dual-quaternions and kronecker product [166]. |
| cv::CirclesGridFinderParameters::CirclesGridFinderParameters | ( | ) |
#include <opencv2/calib.hpp>
| double cv::calibrateCamera | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints, | ||
| Size | imageSize, | ||
| InputOutputArray | cameraMatrix, | ||
| InputOutputArray | distCoeffs, | ||
| OutputArrayOfArrays | rvecs, | ||
| OutputArrayOfArrays | tvecs, | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrateCamera( | objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.calibrateCameraExtended( | objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs, stdDeviationsIntrinsics, stdDeviationsExtrinsics, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| double cv::calibrateCamera | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints, | ||
| Size | imageSize, | ||
| InputOutputArray | cameraMatrix, | ||
| InputOutputArray | distCoeffs, | ||
| OutputArrayOfArrays | rvecs, | ||
| OutputArrayOfArrays | tvecs, | ||
| OutputArray | stdDeviationsIntrinsics, | ||
| OutputArray | stdDeviationsExtrinsics, | ||
| OutputArray | perViewErrors, | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrateCamera( | objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.calibrateCameraExtended( | objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs, stdDeviationsIntrinsics, stdDeviationsExtrinsics, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Finds the camera intrinsic and extrinsic parameters from several views of a calibration pattern.
| objectPoints | In the new interface it is a vector of vectors of calibration pattern points in the calibration pattern coordinate space (e.g. std::vector<std::vector<cv::Vec3f>>). The outer vector contains as many elements as the number of pattern views. If the same calibration pattern is shown in each view and it is fully visible, all the vectors will be the same. Although, it is possible to use partially occluded patterns or even different patterns in different views. Then, the vectors will be different. Although the points are 3D, they all lie in the calibration pattern's XY coordinate plane (thus 0 in the Z-coordinate), if the used calibration pattern is a planar rig. In the old interface all the vectors of object points from different views are concatenated together. |
| imagePoints | In the new interface it is a vector of vectors of the projections of calibration pattern points (e.g. std::vector<std::vector<cv::Vec2f>>). imagePoints.size() and objectPoints.size(), and imagePoints[i].size() and objectPoints[i].size() for each i, must be equal, respectively. In the old interface all the vectors of object points from different views are concatenated together. |
| imageSize | Size of the image used only to initialize the camera intrinsic matrix. |
| cameraMatrix | Input/output 3x3 floating-point camera intrinsic matrix \(\cameramatrix{A}\) . If CALIB_USE_INTRINSIC_GUESS and/or CALIB_FIX_ASPECT_RATIO, CALIB_FIX_PRINCIPAL_POINT or CALIB_FIX_FOCAL_LENGTH are specified, some or all of fx, fy, cx, cy must be initialized before calling the function. |
| distCoeffs | Input/output vector of distortion coefficients \(\distcoeffs\). |
| rvecs | Output vector of rotation vectors (Rodrigues ) estimated for each pattern view (e.g. std::vector<cv::Mat>>). That is, each i-th rotation vector together with the corresponding i-th translation vector (see the next output parameter description) brings the calibration pattern from the object coordinate space (in which object points are specified) to the camera coordinate space. In more technical terms, the tuple of the i-th rotation and translation vector performs a change of basis from object coordinate space to camera coordinate space. Due to its duality, this tuple is equivalent to the position of the calibration pattern with respect to the camera coordinate space. |
| tvecs | Output vector of translation vectors estimated for each pattern view, see parameter description above. |
| stdDeviationsIntrinsics | Output vector of standard deviations estimated for intrinsic parameters. Order of deviations values: \((f_x, f_y, c_x, c_y, k_1, k_2, p_1, p_2, k_3, k_4, k_5, k_6 , s_1, s_2, s_3, s_4, \tau_x, \tau_y)\) If one of parameters is not estimated, it's deviation is equals to zero. |
| stdDeviationsExtrinsics | Output vector of standard deviations estimated for extrinsic parameters. Order of deviations values: \((R_0, T_0, \dotsc , R_{M - 1}, T_{M - 1})\) where M is the number of pattern views. \(R_i, T_i\) are concatenated 1x3 vectors. |
| perViewErrors | Output vector of the RMS re-projection error estimated for each pattern view. |
| flags | Different flags that may be zero or a combination of the following values:
|
| criteria | Termination criteria for the iterative optimization algorithm. |
The function estimates the intrinsic camera parameters and extrinsic parameters for each of the views. The algorithm is based on [323] and [39] . The coordinates of 3D object points and their corresponding 2D projections in each view must be specified. That may be achieved by using an object with known geometry and easily detectable feature points. Such an object is called a calibration rig or calibration pattern, and OpenCV has built-in support for a chessboard as a calibration rig (see findChessboardCorners). Currently, initialization of intrinsic parameters (when CALIB_USE_INTRINSIC_GUESS is not set) is only implemented for planar calibration patterns (where Z-coordinates of the object points must be all zeros). 3D calibration rigs can also be used as long as initial cameraMatrix is provided.
The algorithm performs the following steps:
| double cv::calibrateCameraRO | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints, | ||
| Size | imageSize, | ||
| int | iFixedPoint, | ||
| InputOutputArray | cameraMatrix, | ||
| InputOutputArray | distCoeffs, | ||
| OutputArrayOfArrays | rvecs, | ||
| OutputArrayOfArrays | tvecs, | ||
| OutputArray | newObjPoints, | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrateCameraRO( | objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, flags[, criteria]]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.calibrateCameraROExtended( | objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, stdDeviationsObjPoints[, perViewErrors[, flags[, criteria]]]]]]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints, stdDeviationsIntrinsics, stdDeviationsExtrinsics, stdDeviationsObjPoints, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| double cv::calibrateCameraRO | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints, | ||
| Size | imageSize, | ||
| int | iFixedPoint, | ||
| InputOutputArray | cameraMatrix, | ||
| InputOutputArray | distCoeffs, | ||
| OutputArrayOfArrays | rvecs, | ||
| OutputArrayOfArrays | tvecs, | ||
| OutputArray | newObjPoints, | ||
| OutputArray | stdDeviationsIntrinsics, | ||
| OutputArray | stdDeviationsExtrinsics, | ||
| OutputArray | stdDeviationsObjPoints, | ||
| OutputArray | perViewErrors, | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrateCameraRO( | objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, flags[, criteria]]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.calibrateCameraROExtended( | objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, stdDeviationsObjPoints[, perViewErrors[, flags[, criteria]]]]]]]]] | ) -> | retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints, stdDeviationsIntrinsics, stdDeviationsExtrinsics, stdDeviationsObjPoints, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Finds the camera intrinsic and extrinsic parameters from several views of a calibration pattern.
This function is an extension of calibrateCamera with the method of releasing object which was proposed in [260]. In many common cases with inaccurate, unmeasured, roughly planar targets (calibration plates), this method can dramatically improve the precision of the estimated camera parameters. Both the object-releasing method and standard method are supported by this function. Use the parameter iFixedPoint for method selection. In the internal implementation, calibrateCamera is a wrapper for this function.
| objectPoints | Vector of vectors of calibration pattern points in the calibration pattern coordinate space. See calibrateCamera for details. If the method of releasing object to be used, the identical calibration board must be used in each view and it must be fully visible, and all objectPoints[i] must be the same and all points should be roughly close to a plane. The calibration target has to be rigid, or at least static if the camera (rather than the calibration target) is shifted for grabbing images. |
| imagePoints | Vector of vectors of the projections of calibration pattern points. See calibrateCamera for details. |
| imageSize | Size of the image used only to initialize the intrinsic camera matrix. |
| iFixedPoint | The index of the 3D object point in objectPoints[0] to be fixed. It also acts as a switch for calibration method selection. If object-releasing method to be used, pass in the parameter in the range of [1, objectPoints[0].size()-2], otherwise a value out of this range will make standard calibration method selected. Usually the top-right corner point of the calibration board grid is recommended to be fixed when object-releasing method being utilized. According to [260], two other points are also fixed. In this implementation, objectPoints[0].front and objectPoints[0].back.z are used. With object-releasing method, accurate rvecs, tvecs and newObjPoints are only possible if coordinates of these three fixed points are accurate enough. |
| cameraMatrix | Output 3x3 floating-point camera matrix. See calibrateCamera for details. |
| distCoeffs | Output vector of distortion coefficients. See calibrateCamera for details. |
| rvecs | Output vector of rotation vectors estimated for each pattern view. See calibrateCamera for details. |
| tvecs | Output vector of translation vectors estimated for each pattern view. |
| newObjPoints | The updated output vector of calibration pattern points. The coordinates might be scaled based on three fixed points. The returned coordinates are accurate only if the above mentioned three fixed points are accurate. If not needed, noArray() can be passed in. This parameter is ignored with standard calibration method. |
| stdDeviationsIntrinsics | Output vector of standard deviations estimated for intrinsic parameters. See calibrateCamera for details. |
| stdDeviationsExtrinsics | Output vector of standard deviations estimated for extrinsic parameters. See calibrateCamera for details. |
| stdDeviationsObjPoints | Output vector of standard deviations estimated for refined coordinates of calibration pattern points. It has the same size and order as objectPoints[0] vector. This parameter is ignored with standard calibration method. |
| perViewErrors | Output vector of the RMS re-projection error estimated for each pattern view. |
| flags | Different flags that may be zero or a combination of some predefined values. See calibrateCamera for details. If the method of releasing object is used, the calibration time may be much longer. CALIB_USE_QR or CALIB_USE_LU could be used for faster calibration with potentially less precise and less stable in some rare cases. |
| criteria | Termination criteria for the iterative optimization algorithm. |
The function estimates the intrinsic camera parameters and extrinsic parameters for each of the views. The algorithm is based on [323], [39] and [260]. See calibrateCamera for other detailed explanations.
| void cv::calibrateHandEye | ( | InputArrayOfArrays | R_gripper2base, |
| InputArrayOfArrays | t_gripper2base, | ||
| InputArrayOfArrays | R_target2cam, | ||
| InputArrayOfArrays | t_target2cam, | ||
| OutputArray | R_cam2gripper, | ||
| OutputArray | t_cam2gripper, | ||
| HandEyeCalibrationMethod | method = CALIB_HAND_EYE_TSAI ) |
#include <opencv2/calib.hpp>
Computes Hand-Eye calibration: \(_{}^{g}\textrm{T}_c\).
| [in] | R_gripper2base | Rotation part extracted from the homogeneous matrix that transforms a point expressed in the gripper frame to the robot base frame ( \(_{}^{b}\textrm{T}_g\)). This is a vector (vector<Mat>) that contains the rotation, (3x3) rotation matrices or (3x1) rotation vectors, for all the transformations from gripper frame to robot base frame. |
| [in] | t_gripper2base | Translation part extracted from the homogeneous matrix that transforms a point expressed in the gripper frame to the robot base frame ( \(_{}^{b}\textrm{T}_g\)). This is a vector (vector<Mat>) that contains the (3x1) translation vectors for all the transformations from gripper frame to robot base frame. |
| [in] | R_target2cam | Rotation part extracted from the homogeneous matrix that transforms a point expressed in the target frame to the camera frame ( \(_{}^{c}\textrm{T}_t\)). This is a vector (vector<Mat>) that contains the rotation, (3x3) rotation matrices or (3x1) rotation vectors, for all the transformations from calibration target frame to camera frame. |
| [in] | t_target2cam | Rotation part extracted from the homogeneous matrix that transforms a point expressed in the target frame to the camera frame ( \(_{}^{c}\textrm{T}_t\)). This is a vector (vector<Mat>) that contains the (3x1) translation vectors for all the transformations from calibration target frame to camera frame. |
| [out] | R_cam2gripper | Estimated (3x3) rotation part extracted from the homogeneous matrix that transforms a point expressed in the camera frame to the gripper frame ( \(_{}^{g}\textrm{T}_c\)). |
| [out] | t_cam2gripper | Estimated (3x1) translation part extracted from the homogeneous matrix that transforms a point expressed in the camera frame to the gripper frame ( \(_{}^{g}\textrm{T}_c\)). |
| [in] | method | One of the implemented Hand-Eye calibration method, see cv::HandEyeCalibrationMethod |
The function performs the Hand-Eye calibration using various methods. One approach consists in estimating the rotation then the translation (separable solutions) and the following methods are implemented:
Another approach consists in estimating simultaneously the rotation and the translation (simultaneous solutions), with the following implemented methods:
The following picture describes the Hand-Eye calibration problem where the transformation between a camera ("eye") mounted on a robot gripper ("hand") has to be estimated. This configuration is called eye-in-hand.
The eye-to-hand configuration consists in a static camera observing a calibration pattern mounted on the robot end-effector. The transformation from the camera to the robot base frame can then be estimated by inputting the suitable transformations to the function, see below.

The calibration procedure is the following:
\[ \begin{bmatrix} X_b\\ Y_b\\ Z_b\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{b}\textrm{R}_g & _{}^{b}\textrm{t}_g \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} \]
\[ \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{c}\textrm{R}_t & _{}^{c}\textrm{t}_t \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_t\\ Y_t\\ Z_t\\ 1 \end{bmatrix} \]
The Hand-Eye calibration procedure returns the following homogeneous transformation
\[ \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{g}\textrm{R}_c & _{}^{g}\textrm{t}_c \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} \]
This problem is also known as solving the \(\mathbf{A}\mathbf{X}=\mathbf{X}\mathbf{B}\) equation:
\[ \begin{align*} ^{b}{\textrm{T}_g}^{(1)} \hspace{0.2em} ^{g}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(1)} &= \hspace{0.1em} ^{b}{\textrm{T}_g}^{(2)} \hspace{0.2em} ^{g}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} \\ (^{b}{\textrm{T}_g}^{(2)})^{-1} \hspace{0.2em} ^{b}{\textrm{T}_g}^{(1)} \hspace{0.2em} ^{g}\textrm{T}_c &= \hspace{0.1em} ^{g}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} (^{c}{\textrm{T}_t}^{(1)})^{-1} \\ \textrm{A}_i \textrm{X} &= \textrm{X} \textrm{B}_i \\ \end{align*} \]
\[ \begin{align*} ^{g}{\textrm{T}_b}^{(1)} \hspace{0.2em} ^{b}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(1)} &= \hspace{0.1em} ^{g}{\textrm{T}_b}^{(2)} \hspace{0.2em} ^{b}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} \\ (^{g}{\textrm{T}_b}^{(2)})^{-1} \hspace{0.2em} ^{g}{\textrm{T}_b}^{(1)} \hspace{0.2em} ^{b}\textrm{T}_c &= \hspace{0.1em} ^{b}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} (^{c}{\textrm{T}_t}^{(1)})^{-1} \\ \textrm{A}_i \textrm{X} &= \textrm{X} \textrm{B}_i \\ \end{align*} \]
| double cv::calibrateMultiview | ( | InputArrayOfArrays | objPoints, |
| const std::vector< std::vector< Mat > > & | imagePoints, | ||
| const std::vector< cv::Size > & | imageSize, | ||
| InputArray | detectionMask, | ||
| InputArray | models, | ||
| InputOutputArrayOfArrays | Ks, | ||
| InputOutputArrayOfArrays | distortions, | ||
| InputOutputArrayOfArrays | Rs, | ||
| InputOutputArrayOfArrays | Ts, | ||
| InputArray | flagsForIntrinsics = noArray(), | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrateMultiview( | objPoints, imagePoints, imageSize, detectionMask, models, Ks, distortions, Rs, Ts[, flagsForIntrinsics[, flags[, criteria]]] | ) -> | retval, Ks, distortions, Rs, Ts | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.calibrateMultiviewExtended( | objPoints, imagePoints, imageSize, detectionMask, models, Ks, distortions, Rs, Ts[, initializationPairs[, rvecs0[, tvecs0[, perFrameErrors[, flagsForIntrinsics[, flags[, criteria]]]]]]] | ) -> | retval, Ks, distortions, Rs, Ts, initializationPairs, rvecs0, tvecs0, perFrameErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| double cv::calibrateMultiview | ( | InputArrayOfArrays | objPoints, |
| const std::vector< std::vector< Mat > > & | imagePoints, | ||
| const std::vector< cv::Size > & | imageSize, | ||
| InputArray | detectionMask, | ||
| InputArray | models, | ||
| InputOutputArrayOfArrays | Ks, | ||
| InputOutputArrayOfArrays | distortions, | ||
| InputOutputArrayOfArrays | Rs, | ||
| InputOutputArrayOfArrays | Ts, | ||
| OutputArray | initializationPairs, | ||
| OutputArrayOfArrays | rvecs0, | ||
| OutputArrayOfArrays | tvecs0, | ||
| OutputArray | perFrameErrors, | ||
| InputArray | flagsForIntrinsics = noArray(), | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, DBL_EPSILON) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrateMultiview( | objPoints, imagePoints, imageSize, detectionMask, models, Ks, distortions, Rs, Ts[, flagsForIntrinsics[, flags[, criteria]]] | ) -> | retval, Ks, distortions, Rs, Ts | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.calibrateMultiviewExtended( | objPoints, imagePoints, imageSize, detectionMask, models, Ks, distortions, Rs, Ts[, initializationPairs[, rvecs0[, tvecs0[, perFrameErrors[, flagsForIntrinsics[, flags[, criteria]]]]]]] | ) -> | retval, Ks, distortions, Rs, Ts, initializationPairs, rvecs0, tvecs0, perFrameErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Estimates intrinsics and extrinsics (camera pose) for multi-camera system a.k.a multiview calibration.
| [in] | objPoints | Calibration pattern object points. Expected shape: NUM_FRAMES x NUM_POINTS x 3. Supported data type: CV_32F. |
| [in] | imagePoints | Detected pattern points on camera images. Expected shape: NUM_CAMERAS x NUM_FRAMES x NUM_POINTS x 2. This function supports partial observation of the calibration pattern. To enable this, set the unobserved image points to be invalid points (eg. (-1., -1.)). |
| [in] | imageSize | Images resolution array for each camera. |
| [in] | detectionMask | Pattern detection mask. Each value defines if i-camera observes the calibration pattern in j-th frame. Expected size: NUM_CAMERAS x NUM_FRAMES. Expected type: CV_8U. |
| [in] | models | indicates camera models for each camera: cv::CALIB_MODEL_PINHOLE or cv::CALIB_MODEL_PINHOLE. Current implementation does not support mix of different camera models. Expected type: CV_8U. |
| [in] | flagsForIntrinsics | Flags used for each camera intrinsics calibration. Use per-camera call and the useIntrinsicsGuess flag to get custom intrinsics calibration for each camera. |
| [in] | flags | Common multiview calibration flags. cv::CALIB_USE_INTRINSIC_GUESS and cv::CALIB_USE_EXTRINSIC_GUESS are supported. See CALIB_USE_INTRINSIC_GUESS and other CALIB_ constants. Expected shape: NUM_CAMERAS x 1. Supported data type: CV_32S. |
| [out] | Rs | Rotation vectors relative to camera 0, where Rs[0] = 0. Output size: NUM_CAMERAS x 3 x 3. |
| [out] | Ts | Estimated translation vectors relative to camera 0, where Ts[0] = 0. Output size: NUM_CAMERAS x 3 x 1. |
| [out] | rvecs0 | Estimated rotation vectors for camera 0. Output size: NUM_FRAMES x 3 x 1 (may contain null Mat, if the frame is not valid). See Rodrigues. |
| [out] | tvecs0 | Translation vectors for camera 0. Output size: NUM_FRAMES x 3 x 1. (may contain null Mat, if the frame is not valid). |
| [out] | Ks | Estimated floating-point camera intrinsic matrix. Output size: NUM_CAMERAS x 3 x 3. |
| [out] | distortions | Distortion coefficients. Output size: NUM_CAMERAS x NUM_PARAMS. |
| [out] | perFrameErrors | RMSE value for each visible frame, (-1 for non-visible). Output size: NUM_CAMERAS x NUM_FRAMES. |
| [out] | initializationPairs | Pairs with camera indices that were used for initial pairwise stereo calibration. |
| [in] | criteria | Termination criteria for the iterative optimization algorithm. |
Output size: (NUM_CAMERAS-1) x 2.
Multi-view Camera Calibration Tutorial provides a detailed tutorial of using this function. Please refer to it for more information.
Multiview calibration usually requires several cameras to observe the same calibration pattern simultaneously. The fundamental assumption is that relative camera poses are fixed, and then for each frame, only the absolute camera pose for a single camera is needed to fix the camera pose for the multiple cameras

The above illustration shows an example setting for multiview camera calibration.
For each frame, suppose the absolute camera pose for camera \(i\) is \(R_i, t_i\), and the relative camera pose between camera \(i\) and camera \(j\) is \(R_{ij}, t_{ij}\). Suppose \(R_1, t_1\), and \(R_{1i}\) for any \(i\not=1\) are known, then its pose can be calculated by
\[ R_i = R_{1i} R_1\]
\[ t_i = R_{1i} t_1 + t_{1i}\]
Since the relative pose between two cameras can be calculated by
\[ R_{ij} = R_j R_i^\top \]
\[ t_{ij} = -R_{ij} t_i + R_j \]
This implies that any other relative pose of the form \(R_{ij}, i\not=1\) is redundant. Given this, the total number of poses to determine is (NUM_CAMERAS-1) and NUM_FRAMES. This serves as the foundation of this function.
Similarly to calibrateCamera, the function minimizes the total re-projection error for all the points in all the available views from all cameras.
| void cv::calibrateRobotWorldHandEye | ( | InputArrayOfArrays | R_world2cam, |
| InputArrayOfArrays | t_world2cam, | ||
| InputArrayOfArrays | R_base2gripper, | ||
| InputArrayOfArrays | t_base2gripper, | ||
| OutputArray | R_base2world, | ||
| OutputArray | t_base2world, | ||
| OutputArray | R_gripper2cam, | ||
| OutputArray | t_gripper2cam, | ||
| RobotWorldHandEyeCalibrationMethod | method = CALIB_ROBOT_WORLD_HAND_EYE_SHAH ) |
#include <opencv2/calib.hpp>
Computes Robot-World/Hand-Eye calibration: \(_{}^{w}\textrm{T}_b\) and \(_{}^{c}\textrm{T}_g\).
| [in] | R_world2cam | Rotation part extracted from the homogeneous matrix that transforms a point expressed in the world frame to the camera frame ( \(_{}^{c}\textrm{T}_w\)). This is a vector (vector<Mat>) that contains the rotation, (3x3) rotation matrices or (3x1) rotation vectors, for all the transformations from world frame to the camera frame. |
| [in] | t_world2cam | Translation part extracted from the homogeneous matrix that transforms a point expressed in the world frame to the camera frame ( \(_{}^{c}\textrm{T}_w\)). This is a vector (vector<Mat>) that contains the (3x1) translation vectors for all the transformations from world frame to the camera frame. |
| [in] | R_base2gripper | Rotation part extracted from the homogeneous matrix that transforms a point expressed in the robot base frame to the gripper frame ( \(_{}^{g}\textrm{T}_b\)). This is a vector (vector<Mat>) that contains the rotation, (3x3) rotation matrices or (3x1) rotation vectors, for all the transformations from robot base frame to the gripper frame. |
| [in] | t_base2gripper | Rotation part extracted from the homogeneous matrix that transforms a point expressed in the robot base frame to the gripper frame ( \(_{}^{g}\textrm{T}_b\)). This is a vector (vector<Mat>) that contains the (3x1) translation vectors for all the transformations from robot base frame to the gripper frame. |
| [out] | R_base2world | Estimated (3x3) rotation part extracted from the homogeneous matrix that transforms a point expressed in the robot base frame to the world frame ( \(_{}^{w}\textrm{T}_b\)). |
| [out] | t_base2world | Estimated (3x1) translation part extracted from the homogeneous matrix that transforms a point expressed in the robot base frame to the world frame ( \(_{}^{w}\textrm{T}_b\)). |
| [out] | R_gripper2cam | Estimated (3x3) rotation part extracted from the homogeneous matrix that transforms a point expressed in the gripper frame to the camera frame ( \(_{}^{c}\textrm{T}_g\)). |
| [out] | t_gripper2cam | Estimated (3x1) translation part extracted from the homogeneous matrix that transforms a point expressed in the gripper frame to the camera frame ( \(_{}^{c}\textrm{T}_g\)). |
| [in] | method | One of the implemented Robot-World/Hand-Eye calibration method, see cv::RobotWorldHandEyeCalibrationMethod |
The function performs the Robot-World/Hand-Eye calibration using various methods. One approach consists in estimating the rotation then the translation (separable solutions):
Another approach consists in estimating simultaneously the rotation and the translation (simultaneous solutions), with the following implemented method:
The following picture describes the Robot-World/Hand-Eye calibration problem where the transformations between a robot and a world frame and between a robot gripper ("hand") and a camera ("eye") mounted at the robot end-effector have to be estimated.

The calibration procedure is the following:
\[ \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{g}\textrm{R}_b & _{}^{g}\textrm{t}_b \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_b\\ Y_b\\ Z_b\\ 1 \end{bmatrix} \]
\[ \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{c}\textrm{R}_w & _{}^{c}\textrm{t}_w \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\\ Z_w\\ 1 \end{bmatrix} \]
The Robot-World/Hand-Eye calibration procedure returns the following homogeneous transformations
\[ \begin{bmatrix} X_w\\ Y_w\\ Z_w\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{w}\textrm{R}_b & _{}^{w}\textrm{t}_b \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_b\\ Y_b\\ Z_b\\ 1 \end{bmatrix} \]
\[ \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{c}\textrm{R}_g & _{}^{c}\textrm{t}_g \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} \]
This problem is also known as solving the \(\mathbf{A}\mathbf{X}=\mathbf{Z}\mathbf{B}\) equation, with:
| void cv::calibrationMatrixValues | ( | InputArray | cameraMatrix, |
| Size | imageSize, | ||
| double | apertureWidth, | ||
| double | apertureHeight, | ||
| double & | fovx, | ||
| double & | fovy, | ||
| double & | focalLength, | ||
| Point2d & | principalPoint, | ||
| double & | aspectRatio ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.calibrationMatrixValues( | cameraMatrix, imageSize, apertureWidth, apertureHeight | ) -> | fovx, fovy, focalLength, principalPoint, aspectRatio | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Computes useful camera characteristics from the camera intrinsic matrix.
| cameraMatrix | Input camera intrinsic matrix that can be estimated by calibrateCamera or stereoCalibrate . |
| imageSize | Input image size in pixels. |
| apertureWidth | Physical width in mm of the sensor. |
| apertureHeight | Physical height in mm of the sensor. |
| fovx | Output field of view in degrees along the horizontal sensor axis. |
| fovy | Output field of view in degrees along the vertical sensor axis. |
| focalLength | Focal length of the lens in mm. |
| principalPoint | Principal point in mm. |
| aspectRatio | \(f_y/f_x\) |
The function computes various useful camera characteristics from the previously estimated camera matrix.
| bool cv::checkChessboard | ( | InputArray | img, |
| Size | size ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.checkChessboard( | img, size | ) -> | retval | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
| void cv::drawChessboardCorners | ( | InputOutputArray | image, |
| Size | patternSize, | ||
| InputArray | corners, | ||
| bool | patternWasFound ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.drawChessboardCorners( | image, patternSize, corners, patternWasFound | ) -> | image | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Renders the detected chessboard corners.
| image | Destination image. It must be an 8-bit color image. |
| patternSize | Number of inner corners per a chessboard row and column (patternSize = cv::Size(points_per_row,points_per_column)). |
| corners | Array of detected corners, the output of findChessboardCorners. |
| patternWasFound | Parameter indicating whether the complete board was found or not. The return value of findChessboardCorners should be passed here. |
The function draws individual chessboard corners detected either as red circles if the board was not found, or as colored corners connected with lines if the board was found.
| Scalar cv::estimateChessboardSharpness | ( | InputArray | image, |
| Size | patternSize, | ||
| InputArray | corners, | ||
| float | rise_distance = 0.8F, | ||
| bool | vertical = false, | ||
| OutputArray | sharpness = noArray() ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.estimateChessboardSharpness( | image, patternSize, corners[, rise_distance[, vertical[, sharpness]]] | ) -> | retval, sharpness | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Estimates the sharpness of a detected chessboard.
Image sharpness, as well as brightness, are a critical parameter for accuracte camera calibration. For accessing these parameters for filtering out problematic calibraiton images, this method calculates edge profiles by traveling from black to white chessboard cell centers. Based on this, the number of pixels is calculated required to transit from black to white. This width of the transition area is a good indication of how sharp the chessboard is imaged and should be below ~3.0 pixels.
| image | Gray image used to find chessboard corners |
| patternSize | Size of a found chessboard pattern |
| corners | Corners found by findChessboardCornersSB |
| rise_distance | Rise distance 0.8 means 10% ... 90% of the final signal strength |
| vertical | By default edge responses for horizontal lines are calculated |
| sharpness | Optional output array with a sharpness value for calculated edge responses (see description) |
The optional sharpness array is of type CV_32FC1 and has for each calculated profile one row with the following five entries: 0 = x coordinate of the underlying edge in the image 1 = y coordinate of the underlying edge in the image 2 = width of the transition area (sharpness) 3 = signal strength in the black cell (min brightness) 4 = signal strength in the white cell (max brightness)
| bool cv::find4QuadCornerSubpix | ( | InputArray | img, |
| InputOutputArray | corners, | ||
| Size | region_size ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.find4QuadCornerSubpix( | img, corners, region_size | ) -> | retval, corners | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
finds subpixel-accurate positions of the chessboard corners
| bool cv::findChessboardCorners | ( | InputArray | image, |
| Size | patternSize, | ||
| OutputArray | corners, | ||
| int | flags = CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.findChessboardCorners( | image, patternSize[, corners[, flags]] | ) -> | retval, corners | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Finds the positions of internal corners of the chessboard.
| image | Source chessboard view. It must be an 8-bit grayscale or color image. |
| patternSize | Number of inner corners per a chessboard row and column ( patternSize = cv::Size(points_per_row,points_per_colum) = cv::Size(columns,rows) ). |
| corners | Output array of detected corners. |
| flags | Various operation flags that can be zero or a combination of the following values:
|
The function attempts to determine whether the input image is a view of the chessboard pattern and locate the internal chessboard corners. The function returns a non-zero value if all of the corners are found and they are placed in a certain order (row by row, left to right in every row). Otherwise, if the function fails to find all the corners or reorder them, it returns 0. For example, a regular chessboard has 8 x 8 squares and 7 x 7 internal corners, that is, points where the black squares touch each other. The detected coordinates are approximate, and to determine their positions more accurately, the function calls cornerSubPix. You also may use the function cornerSubPix with different parameters if returned coordinates are not accurate enough.
Sample usage of detecting and drawing chessboard corners: :
Use the generate_pattern.py Python script (Create Calibration Pattern) to create the desired checkerboard pattern.
| bool cv::findChessboardCornersSB | ( | InputArray | image, |
| Size | patternSize, | ||
| OutputArray | corners, | ||
| int | flags, | ||
| OutputArray | meta ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.findChessboardCornersSB( | image, patternSize[, corners[, flags]] | ) -> | retval, corners | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.findChessboardCornersSBWithMeta( | image, patternSize, flags[, corners[, meta]] | ) -> | retval, corners, meta | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Finds the positions of internal corners of the chessboard using a sector based approach.
| image | Source chessboard view. It must be an 8-bit grayscale or color image. |
| patternSize | Number of inner corners per a chessboard row and column ( patternSize = cv::Size(points_per_row,points_per_colum) = cv::Size(columns,rows) ). |
| corners | Output array of detected corners. |
| flags | Various operation flags that can be zero or a combination of the following values:
|
| meta | Optional output arrray of detected corners (CV_8UC1 and size = cv::Size(columns,rows)). Each entry stands for one corner of the pattern and can have one of the following values:
|
The function is analog to findChessboardCorners but uses a localized radon transformation approximated by box filters being more robust to all sort of noise, faster on larger images and is able to directly return the sub-pixel position of the internal chessboard corners. The Method is based on the paper [78] "Accurate Detection and Localization of Checkerboard Corners for Calibration" demonstrating that the returned sub-pixel positions are more accurate than the one returned by cornerSubPix allowing a precise camera calibration for demanding applications.
In the case, the flags CALIB_CB_LARGER or CALIB_CB_MARKER are given, the result can be recovered from the optional meta array. Both flags are helpful to use calibration patterns exceeding the field of view of the camera. These oversized patterns allow more accurate calibrations as corners can be utilized, which are as close as possible to the image borders. For a consistent coordinate system across all images, the optional marker (see image below) can be used to move the origin of the board to the location where the black circle is located.
Use the generate_pattern.py Python script (Create Calibration Pattern) to create the corresponding checkerboard pattern:

|
inline |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.findChessboardCornersSB( | image, patternSize[, corners[, flags]] | ) -> | retval, corners | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.findChessboardCornersSBWithMeta( | image, patternSize, flags[, corners[, meta]] | ) -> | retval, corners, meta | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| bool cv::findCirclesGrid | ( | InputArray | image, |
| Size | patternSize, | ||
| OutputArray | centers, | ||
| int | flags, | ||
| const Ptr< FeatureDetector > & | blobDetector, | ||
| const CirclesGridFinderParameters & | parameters ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.findCirclesGrid( | image, patternSize, flags, blobDetector, parameters[, centers] | ) -> | retval, centers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.findCirclesGrid( | image, patternSize[, centers[, flags[, blobDetector]]] | ) -> | retval, centers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Finds centers in the grid of circles.
| image | grid view of input circles; it must be an 8-bit grayscale or color image. |
| patternSize | number of circles per row and column ( patternSize = Size(points_per_row, points_per_colum) ). |
| centers | output array of detected centers. |
| flags | various operation flags that can be one of the following values:
|
| blobDetector | feature detector that finds blobs like dark circles on light background. If blobDetector is NULL then image represents Point2f array of candidates. |
| parameters | struct for finding circles in a grid pattern. |
The function attempts to determine whether the input image contains a grid of circles. If it is, the function locates centers of the circles. The function returns a non-zero value if all of the centers have been found and they have been placed in a certain order (row by row, left to right in every row). Otherwise, if the function fails to find all the corners or reorder them, it returns 0.
Sample usage of detecting and drawing the centers of circles: :
| bool cv::findCirclesGrid | ( | InputArray | image, |
| Size | patternSize, | ||
| OutputArray | centers, | ||
| int | flags = CALIB_CB_SYMMETRIC_GRID, | ||
| const Ptr< FeatureDetector > & | blobDetector = SimpleBlobDetector::create() ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.findCirclesGrid( | image, patternSize, flags, blobDetector, parameters[, centers] | ) -> | retval, centers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.findCirclesGrid( | image, patternSize[, centers[, flags[, blobDetector]]] | ) -> | retval, centers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| Mat cv::initCameraMatrix2D | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints, | ||
| Size | imageSize, | ||
| double | aspectRatio = 1.0 ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.initCameraMatrix2D( | objectPoints, imagePoints, imageSize[, aspectRatio] | ) -> | retval | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Finds an initial camera intrinsic matrix from 3D-2D point correspondences.
| objectPoints | Vector of vectors of the calibration pattern points in the calibration pattern coordinate space. In the old interface all the per-view vectors are concatenated. See calibrateCamera for details. |
| imagePoints | Vector of vectors of the projections of the calibration pattern points. In the old interface all the per-view vectors are concatenated. |
| imageSize | Image size in pixels used to initialize the principal point. |
| aspectRatio | If it is zero or negative, both \(f_x\) and \(f_y\) are estimated independently. Otherwise, \(f_x = f_y \cdot \texttt{aspectRatio}\) . |
The function estimates and returns an initial camera intrinsic matrix for the camera calibration process. Currently, the function only supports planar calibration patterns, which are patterns where each object point has z-coordinate =0.
| double cv::registerCameras | ( | InputArrayOfArrays | objectPoints1, |
| InputArrayOfArrays | objectPoints2, | ||
| InputArrayOfArrays | imagePoints1, | ||
| InputArrayOfArrays | imagePoints2, | ||
| InputArray | cameraMatrix1, | ||
| InputArray | distCoeffs1, | ||
| CameraModel | cameraModel1, | ||
| InputArray | cameraMatrix2, | ||
| InputArray | distCoeffs2, | ||
| CameraModel | cameraModel2, | ||
| InputOutputArray | R, | ||
| InputOutputArray | T, | ||
| OutputArray | E, | ||
| OutputArray | F, | ||
| OutputArray | perViewErrors, | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.registerCameras( | objectPoints1, objectPoints2, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraModel1, cameraMatrix2, distCoeffs2, cameraModel2, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]] | ) -> | retval, R, T, E, F, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.registerCamerasExtended( | objectPoints1, objectPoints2, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraModel1, cameraMatrix2, distCoeffs2, cameraModel2, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, R, T, E, F, rvecs, tvecs, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| double cv::registerCameras | ( | InputArrayOfArrays | objectPoints1, |
| InputArrayOfArrays | objectPoints2, | ||
| InputArrayOfArrays | imagePoints1, | ||
| InputArrayOfArrays | imagePoints2, | ||
| InputArray | cameraMatrix1, | ||
| InputArray | distCoeffs1, | ||
| CameraModel | cameraModel1, | ||
| InputArray | cameraMatrix2, | ||
| InputArray | distCoeffs2, | ||
| CameraModel | cameraModel2, | ||
| InputOutputArray | R, | ||
| InputOutputArray | T, | ||
| OutputArray | E, | ||
| OutputArray | F, | ||
| OutputArrayOfArrays | rvecs, | ||
| OutputArrayOfArrays | tvecs, | ||
| OutputArray | perViewErrors, | ||
| int | flags = 0, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.registerCameras( | objectPoints1, objectPoints2, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraModel1, cameraMatrix2, distCoeffs2, cameraModel2, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]] | ) -> | retval, R, T, E, F, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.registerCamerasExtended( | objectPoints1, objectPoints2, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraModel1, cameraMatrix2, distCoeffs2, cameraModel2, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, R, T, E, F, rvecs, tvecs, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Calibrates a camera pair set up. This function finds the extrinsic parameters between the two cameras.
| objectPoints1 | Vector of vectors of the calibration pattern points for camera 1. A similar structure as objectPoints in calibrateCamera and for each pattern view, both cameras do not need to see the same object points. objectPoints1.size(), imagePoints1.size() nees to be equal,as well as objectPoints1[i].size(), imagePoints1[i].size() need to be equal for each i. |
| objectPoints2 | Vector of vectors of the calibration pattern points for camera 2. A similar structure as objectPoints1. objectPoints2.size(), and imagePoints2.size() nees to be equal, as well as objectPoints2[i].size(), imagePoints2[i].size() need to be equal for each i. However, objectPoints1[i].size() and objectPoints2[i].size() are not required to be equal. |
| imagePoints1 | Vector of vectors of the projections of the calibration pattern points, observed by the first camera. The same structure as in calibrateCamera. |
| imagePoints2 | Vector of vectors of the projections of the calibration pattern points, observed by the second camera. The same structure as in calibrateCamera. |
| cameraMatrix1 | Input/output camera intrinsic matrix for the first camera, the same as in calibrateCamera. Furthermore, for the stereo case, additional flags may be used, see below. |
| distCoeffs1 | Input/output vector of distortion coefficients, the same as in calibrateCamera. |
| cameraModel1 | Flag reflecting the type of model for camera 1 (pinhole / fisheye):
|
| cameraMatrix2 | Input/output second camera intrinsic matrix for the second camera. See description for cameraMatrix1. |
| distCoeffs2 | Input/output lens distortion coefficients for the second camera. See description for distCoeffs1. |
| cameraModel2 | Flag reflecting the type of model for camera 2 (pinhole / fisheye). See description for cameraModel1. |
| R | Output rotation matrix. Together with the translation vector T, this matrix brings points given in the first camera's coordinate system to points in the second camera's coordinate system. In more technical terms, the tuple of R and T performs a change of basis from the first camera's coordinate system to the second camera's coordinate system. Due to its duality, this tuple is equivalent to the position of the first camera with respect to the second camera coordinate system. |
| T | Output translation vector, see description above. |
| E | Output essential matrix. |
| F | Output fundamental matrix. |
| rvecs | Output vector of rotation vectors ( Rodrigues ) estimated for each pattern view in the coordinate system of the first camera of the stereo pair (e.g. std::vector<cv::Mat>). More in detail, each i-th rotation vector together with the corresponding i-th translation vector (see the next output parameter description) brings the calibration pattern from the object coordinate space (in which object points are specified) to the camera coordinate space of the first camera of the stereo pair. In more technical terms, the tuple of the i-th rotation and translation vector performs a change of basis from object coordinate space to the camera coordinate space of the first camera of the stereo pair. |
| tvecs | Output vector of translation vectors estimated for each pattern view, see parameter description of previous output parameter ( rvecs ). |
| perViewErrors | Output vector of the RMS re-projection error estimated for each pattern view. |
| flags | Different flags that may be zero or a combination of the following values:
|
| criteria | Termination criteria for the iterative optimization algorithm. |
The function estimates the transformation between two cameras similar to stereo pair calibration. The principle follows closely to stereoCalibrate. To understand the problem of estimating the relative pose between a camera pair, please refer to the description there. The difference for this function is that, camera intrinsics are not optimized and two cameras are not required to have overlapping fields of view as long as they are observing the same calibration target and the absolute positions of each object point are known. 
The above illustration shows an example where such a case may become relevant. Additionally, it supports a camera pair with the mixed model (pinhole / fisheye). Similarly to calibrateCamera, the function minimizes the total re-projection error for all the points in all the available views from both cameras.
| double cv::stereoCalibrate | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints1, | ||
| InputArrayOfArrays | imagePoints2, | ||
| InputOutputArray | cameraMatrix1, | ||
| InputOutputArray | distCoeffs1, | ||
| InputOutputArray | cameraMatrix2, | ||
| InputOutputArray | distCoeffs2, | ||
| Size | imageSize, | ||
| InputOutputArray | R, | ||
| InputOutputArray | T, | ||
| OutputArray | E, | ||
| OutputArray | F, | ||
| OutputArray | perViewErrors, | ||
| int | flags = CALIB_FIX_INTRINSIC, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.stereoCalibrate( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize[, R[, T[, E[, F[, flags[, criteria]]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.stereoCalibrate( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.stereoCalibrateExtended( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, rvecs, tvecs, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| double cv::stereoCalibrate | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints1, | ||
| InputArrayOfArrays | imagePoints2, | ||
| InputOutputArray | cameraMatrix1, | ||
| InputOutputArray | distCoeffs1, | ||
| InputOutputArray | cameraMatrix2, | ||
| InputOutputArray | distCoeffs2, | ||
| Size | imageSize, | ||
| InputOutputArray | R, | ||
| InputOutputArray | T, | ||
| OutputArray | E, | ||
| OutputArray | F, | ||
| OutputArrayOfArrays | rvecs, | ||
| OutputArrayOfArrays | tvecs, | ||
| OutputArray | perViewErrors, | ||
| int | flags = CALIB_FIX_INTRINSIC, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.stereoCalibrate( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize[, R[, T[, E[, F[, flags[, criteria]]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.stereoCalibrate( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.stereoCalibrateExtended( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, rvecs, tvecs, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
Calibrates a stereo camera set up. This function finds the intrinsic parameters for each of the two cameras and the extrinsic parameters between the two cameras.
| objectPoints | Vector of vectors of the calibration pattern points. The same structure as in calibrateCamera. For each pattern view, both cameras need to see the same object points. Therefore, objectPoints.size(), imagePoints1.size(), and imagePoints2.size() need to be equal as well as objectPoints[i].size(), imagePoints1[i].size(), and imagePoints2[i].size() need to be equal for each i. |
| imagePoints1 | Vector of vectors of the projections of the calibration pattern points, observed by the first camera. The same structure as in calibrateCamera. |
| imagePoints2 | Vector of vectors of the projections of the calibration pattern points, observed by the second camera. The same structure as in calibrateCamera. |
| cameraMatrix1 | Input/output camera intrinsic matrix for the first camera, the same as in calibrateCamera. Furthermore, for the stereo case, additional flags may be used, see below. |
| distCoeffs1 | Input/output vector of distortion coefficients, the same as in calibrateCamera. |
| cameraMatrix2 | Input/output second camera intrinsic matrix for the second camera. See description for cameraMatrix1. |
| distCoeffs2 | Input/output lens distortion coefficients for the second camera. See description for distCoeffs1. |
| imageSize | Size of the image used only to initialize the camera intrinsic matrices. |
| R | Output rotation matrix. Together with the translation vector T, this matrix brings points given in the first camera's coordinate system to points in the second camera's coordinate system. In more technical terms, the tuple of R and T performs a change of basis from the first camera's coordinate system to the second camera's coordinate system. Due to its duality, this tuple is equivalent to the position of the first camera with respect to the second camera coordinate system. |
| T | Output translation vector, see description above. |
| E | Output essential matrix. |
| F | Output fundamental matrix. |
| rvecs | Output vector of rotation vectors ( Rodrigues ) estimated for each pattern view in the coordinate system of the first camera of the stereo pair (e.g. std::vector<cv::Mat>). More in detail, each i-th rotation vector together with the corresponding i-th translation vector (see the next output parameter description) brings the calibration pattern from the object coordinate space (in which object points are specified) to the camera coordinate space of the first camera of the stereo pair. In more technical terms, the tuple of the i-th rotation and translation vector performs a change of basis from object coordinate space to camera coordinate space of the first camera of the stereo pair. |
| tvecs | Output vector of translation vectors estimated for each pattern view, see parameter description of previous output parameter ( rvecs ). |
| perViewErrors | Output vector of the RMS re-projection error estimated for each pattern view. |
| flags | Different flags that may be zero or a combination of the following values:
|
| criteria | Termination criteria for the iterative optimization algorithm. |
The function estimates the transformation between two cameras making a stereo pair. If one computes the poses of an object relative to the first camera and to the second camera, ( \(R_1\), \(T_1\) ) and ( \(R_2\), \(T_2\)), respectively, for a stereo camera where the relative position and orientation between the two cameras are fixed, then those poses definitely relate to each other. This means, if the relative position and orientation ( \(R\), \(T\)) of the two cameras is known, it is possible to compute ( \(R_2\), \(T_2\)) when ( \(R_1\), \(T_1\)) is given. This is what the described function does. It computes ( \(R\), \(T\)) such that:
\[R_2=R R_1\]
\[T_2=R T_1 + T.\]
Therefore, one can compute the coordinate representation of a 3D point for the second camera's coordinate system when given the point's coordinate representation in the first camera's coordinate system:
\[\begin{bmatrix} X_2 \\ Y_2 \\ Z_2 \\ 1 \end{bmatrix} = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix} \begin{bmatrix} X_1 \\ Y_1 \\ Z_1 \\ 1 \end{bmatrix}.\]
Optionally, it computes the essential matrix E:
\[E= \vecthreethree{0}{-T_2}{T_1}{T_2}{0}{-T_0}{-T_1}{T_0}{0} R\]
where \(T_i\) are components of the translation vector \(T\) : \(T=[T_0, T_1, T_2]^T\) . And the function can also compute the fundamental matrix F:
\[F = cameraMatrix2^{-T}\cdot E \cdot cameraMatrix1^{-1}\]
Besides the stereo-related information, the function can also perform a full calibration of each of the two cameras. However, due to the high dimensionality of the parameter space and noise in the input data, the function can diverge from the correct solution. If the intrinsic parameters can be estimated with high accuracy for each of the cameras individually (for example, using calibrateCamera ), you are recommended to do so and then pass CALIB_FIX_INTRINSIC flag to the function along with the computed intrinsic parameters. Otherwise, if all the parameters are estimated at once, it makes sense to restrict some parameters, for example, pass CALIB_SAME_FOCAL_LENGTH and CALIB_ZERO_TANGENT_DIST flags, which is usually a reasonable assumption.
Similarly to calibrateCamera, the function minimizes the total re-projection error for all the points in all the available views from both cameras. The function returns the final value of the re-projection error.
| double cv::stereoCalibrate | ( | InputArrayOfArrays | objectPoints, |
| InputArrayOfArrays | imagePoints1, | ||
| InputArrayOfArrays | imagePoints2, | ||
| InputOutputArray | cameraMatrix1, | ||
| InputOutputArray | distCoeffs1, | ||
| InputOutputArray | cameraMatrix2, | ||
| InputOutputArray | distCoeffs2, | ||
| Size | imageSize, | ||
| OutputArray | R, | ||
| OutputArray | T, | ||
| OutputArray | E, | ||
| OutputArray | F, | ||
| int | flags = CALIB_FIX_INTRINSIC, | ||
| TermCriteria | criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-6) ) |
| Python: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cv.stereoCalibrate( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize[, R[, T[, E[, F[, flags[, criteria]]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.stereoCalibrate( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cv.stereoCalibrateExtended( | objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]] | ) -> | retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, rvecs, tvecs, perViewErrors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
#include <opencv2/calib.hpp>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| float cv::CirclesGridFinderParameters::convexHullFactor |
| cv::Size2f cv::CirclesGridFinderParameters::densityNeighborhoodSize |
| float cv::CirclesGridFinderParameters::edgeGain |
| float cv::CirclesGridFinderParameters::edgePenalty |
| float cv::CirclesGridFinderParameters::existingVertexGain |
| GridType cv::CirclesGridFinderParameters::gridType |
| int cv::CirclesGridFinderParameters::keypointScale |
| int cv::CirclesGridFinderParameters::kmeansAttempts |
| float cv::CirclesGridFinderParameters::maxRectifiedDistance |
Max deviation from prediction. Used by CALIB_CB_CLUSTERING.
| float cv::CirclesGridFinderParameters::minDensity |
| int cv::CirclesGridFinderParameters::minDistanceToAddKeypoint |
| float cv::CirclesGridFinderParameters::minGraphConfidence |
| float cv::CirclesGridFinderParameters::minRNGEdgeSwitchDist |
| float cv::CirclesGridFinderParameters::squareSize |
Distance between two adjacent points. Used by CALIB_CB_CLUSTERING.
| float cv::CirclesGridFinderParameters::vertexGain |
| float cv::CirclesGridFinderParameters::vertexPenalty |