 |
OpenCV
4.5.1
Open Source Computer Vision
|
 |
OpenCV
4.5.1
Open Source Computer Vision
|
Next Tutorial: Shi-Tomasi corner detector
| Original author | Ana Huamán |
| Compatibility | OpenCV >= 3.0 |
In this tutorial you will learn:
To mention a few:
In this tutorial we will study the corner features, specifically.
Consider a grayscale image \(I\). We are going to sweep a window \(w(x,y)\) (with displacements \(u\) in the x direction and \(v\) in the y direction) \(I\) and will calculate the variation of intensity.
\[E(u,v) = \sum _{x,y} w(x,y)[ I(x+u,y+v) - I(x,y)]^{2}\]
where:
Since we are looking for windows with corners, we are looking for windows with a large variation in intensity. Hence, we have to maximize the equation above, specifically the term:
\[\sum _{x,y}[ I(x+u,y+v) - I(x,y)]^{2}\]
Using Taylor expansion:
\[E(u,v) \approx \sum _{x,y}[ I(x,y) + u I_{x} + vI_{y} - I(x,y)]^{2}\]
Expanding the equation and cancelling properly:
\[E(u,v) \approx \sum _{x,y} u^{2}I_{x}^{2} + 2uvI_{x}I_{y} + v^{2}I_{y}^{2}\]
Which can be expressed in a matrix form as:
\[E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} \left ( \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} \right ) \begin{bmatrix} u \\ v \end{bmatrix}\]
Let's denote:
\[M = \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix}\]
So, our equation now is:
\[E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix}\]
A score is calculated for each window, to determine if it can possibly contain a corner:
\[R = det(M) - k(trace(M))^{2}\]
where:
a window with a score \(R\) greater than a certain value is considered a "corner"
The original image:
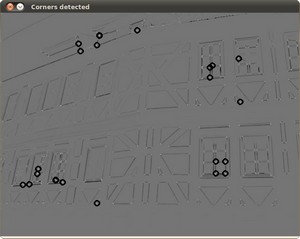
The detected corners are surrounded by a small black circle
 1.8.13
1.8.13