Structural Analysis and Shape Descriptors

Detailed Description

Namespaces
namespace	cv::traits

Classes
class	cv::GeneralizedHough
	finds arbitrary template in the grayscale image using Generalized Hough Transform More...
class	cv::GeneralizedHoughBallard
	finds arbitrary template in the grayscale image using Generalized Hough Transform More...
class	cv::GeneralizedHoughGuil
	finds arbitrary template in the grayscale image using Generalized Hough Transform More...
class	cv::Moments
	struct returned by cv::moments More...

Enumerations
enum	cv::ConnectedComponentsAlgorithmsTypes {   cv::CCL_DEFAULT = -1 ,   cv::CCL_WU = 0 ,   cv::CCL_GRANA = 1 ,   cv::CCL_BOLELLI = 2 ,   cv::CCL_SAUF = 3 ,   cv::CCL_BBDT = 4 ,   cv::CCL_SPAGHETTI = 5 }
	connected components algorithm More...
enum	cv::ConnectedComponentsTypes {   cv::CC_STAT_LEFT = 0 ,   cv::CC_STAT_TOP = 1 ,   cv::CC_STAT_WIDTH = 2 ,   cv::CC_STAT_HEIGHT = 3 ,   cv::CC_STAT_AREA = 4 }
	connected components statistics More...
enum	cv::ContourApproximationModes {   cv::CHAIN_APPROX_NONE = 1 ,   cv::CHAIN_APPROX_SIMPLE = 2 ,   cv::CHAIN_APPROX_TC89_L1 = 3 ,   cv::CHAIN_APPROX_TC89_KCOS = 4 }
	the contour approximation algorithm More...
enum	cv::RectanglesIntersectTypes {   cv::INTERSECT_NONE = 0 ,   cv::INTERSECT_PARTIAL = 1 ,   cv::INTERSECT_FULL = 2 }
	types of intersection between rectangles More...
enum	cv::RetrievalModes {   cv::RETR_EXTERNAL = 0 ,   cv::RETR_LIST = 1 ,   cv::RETR_CCOMP = 2 ,   cv::RETR_TREE = 3 ,   cv::RETR_FLOODFILL = 4 }
	mode of the contour retrieval algorithm More...
enum	cv::ShapeMatchModes {   cv::CONTOURS_MATCH_I1 =1 ,   cv::CONTOURS_MATCH_I2 =2 ,   cv::CONTOURS_MATCH_I3 =3 }
	Shape matching methods. More...

Functions
void	cv::approxPolyDP (InputArray curve, OutputArray approxCurve, double epsilon, bool closed)
	Approximates a polygonal curve(s) with the specified precision.
void	cv::approxPolyN (InputArray curve, OutputArray approxCurve, int nsides, float epsilon_percentage=-1.0, bool ensure_convex=true)
	Approximates a polygon with a convex hull with a specified accuracy and number of sides.
double	cv::arcLength (InputArray curve, bool closed)
	Calculates a contour perimeter or a curve length.
Rect	cv::boundingRect (InputArray array)
	Calculates the up-right bounding rectangle of a point set or non-zero pixels of gray-scale image.
void	cv::boxPoints (RotatedRect box, OutputArray points)
	Finds the four vertices of a rotated rect. Useful to draw the rotated rectangle.
int	cv::connectedComponents (InputArray image, OutputArray labels, int connectivity, int ltype, int ccltype)
	computes the connected components labeled image of boolean image
int	cv::connectedComponents (InputArray image, OutputArray labels, int connectivity=8, int ltype=CV_32S)
int	cv::connectedComponentsWithStats (InputArray image, OutputArray labels, OutputArray stats, OutputArray centroids, int connectivity, int ltype, int ccltype)
	computes the connected components labeled image of boolean image and also produces a statistics output for each label
int	cv::connectedComponentsWithStats (InputArray image, OutputArray labels, OutputArray stats, OutputArray centroids, int connectivity=8, int ltype=CV_32S)
double	cv::contourArea (InputArray contour, bool oriented=false)
	Calculates a contour area.
void	cv::convexHull (InputArray points, OutputArray hull, bool clockwise=false, bool returnPoints=true)
	Finds the convex hull of a point set.
void	cv::convexityDefects (InputArray contour, InputArray convexhull, OutputArray convexityDefects)
	Finds the convexity defects of a contour.
Ptr< GeneralizedHoughBallard >	cv::createGeneralizedHoughBallard ()
	Creates a smart pointer to a cv::GeneralizedHoughBallard class and initializes it.
Ptr< GeneralizedHoughGuil >	cv::createGeneralizedHoughGuil ()
	Creates a smart pointer to a cv::GeneralizedHoughGuil class and initializes it.
void	cv::findContours (InputArray image, OutputArrayOfArrays contours, int mode, int method, Point offset=Point())
void	cv::findContours (InputArray image, OutputArrayOfArrays contours, OutputArray hierarchy, int mode, int method, Point offset=Point())
	Finds contours in a binary image.
void	cv::findContoursLinkRuns (InputArray image, OutputArrayOfArrays contours)
	This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
void	cv::findContoursLinkRuns (InputArray image, OutputArrayOfArrays contours, OutputArray hierarchy)
	Find contours using link runs algorithm.
RotatedRect	cv::fitEllipse (InputArray points)
	Fits an ellipse around a set of 2D points.
RotatedRect	cv::fitEllipseAMS (InputArray points)
	Fits an ellipse around a set of 2D points.
RotatedRect	cv::fitEllipseDirect (InputArray points)
	Fits an ellipse around a set of 2D points.
void	cv::fitLine (InputArray points, OutputArray line, int distType, double param, double reps, double aeps)
	Fits a line to a 2D or 3D point set.
void	cv::HuMoments (const Moments &m, OutputArray hu)
void	cv::HuMoments (const Moments &moments, double hu[7])
	Calculates seven Hu invariants.
float	cv::intersectConvexConvex (InputArray p1, InputArray p2, OutputArray p12, bool handleNested=true)
	Finds intersection of two convex polygons.
bool	cv::isContourConvex (InputArray contour)
	Tests a contour convexity.
double	cv::matchShapes (InputArray contour1, InputArray contour2, int method, double parameter)
	Compares two shapes.
RotatedRect	cv::minAreaRect (InputArray points)
	Finds a rotated rectangle of the minimum area enclosing the input 2D point set.
void	cv::minEnclosingCircle (InputArray points, Point2f &center, float &radius)
	Finds a circle of the minimum area enclosing a 2D point set.
double	cv::minEnclosingTriangle (InputArray points, OutputArray triangle)
	Finds a triangle of minimum area enclosing a 2D point set and returns its area.
Moments	cv::moments (InputArray array, bool binaryImage=false)
	Calculates all of the moments up to the third order of a polygon or rasterized shape.
double	cv::pointPolygonTest (InputArray contour, Point2f pt, bool measureDist)
	Performs a point-in-contour test.
int	cv::rotatedRectangleIntersection (const RotatedRect &rect1, const RotatedRect &rect2, OutputArray intersectingRegion)
	Finds out if there is any intersection between two rotated rectangles.

Enumeration Type Documentation

ConnectedComponentsAlgorithmsTypes

enum cv::ConnectedComponentsAlgorithmsTypes

#include <opencv2/imgproc.hpp>

connected components algorithm

Enumerator
CCL_DEFAULT  Python: cv.CCL_DEFAULT	Spaghetti [31] algorithm for 8-way connectivity, Spaghetti4C [32] algorithm for 4-way connectivity.
CCL_WU  Python: cv.CCL_WU	SAUF [301] algorithm for 8-way connectivity, SAUF algorithm for 4-way connectivity. The parallel implementation described in [30] is available for SAUF.
CCL_GRANA  Python: cv.CCL_GRANA	BBDT [110] algorithm for 8-way connectivity, SAUF algorithm for 4-way connectivity. The parallel implementation described in [30] is available for both BBDT and SAUF.
CCL_BOLELLI  Python: cv.CCL_BOLELLI	Spaghetti [31] algorithm for 8-way connectivity, Spaghetti4C [32] algorithm for 4-way connectivity. The parallel implementation described in [30] is available for both Spaghetti and Spaghetti4C.
CCL_SAUF  Python: cv.CCL_SAUF	Same as CCL_WU. It is preferable to use the flag with the name of the algorithm (CCL_SAUF) rather than the one with the name of the first author (CCL_WU).
CCL_BBDT  Python: cv.CCL_BBDT	Same as CCL_GRANA. It is preferable to use the flag with the name of the algorithm (CCL_BBDT) rather than the one with the name of the first author (CCL_GRANA).
CCL_SPAGHETTI  Python: cv.CCL_SPAGHETTI	Same as CCL_BOLELLI. It is preferable to use the flag with the name of the algorithm (CCL_SPAGHETTI) rather than the one with the name of the first author (CCL_BOLELLI).

ConnectedComponentsTypes

enum cv::ConnectedComponentsTypes

#include <opencv2/imgproc.hpp>

connected components statistics

Enumerator
CC_STAT_LEFT  Python: cv.CC_STAT_LEFT	The leftmost (x) coordinate which is the inclusive start of the bounding box in the horizontal direction.
CC_STAT_TOP  Python: cv.CC_STAT_TOP	The topmost (y) coordinate which is the inclusive start of the bounding box in the vertical direction.
CC_STAT_WIDTH  Python: cv.CC_STAT_WIDTH	The horizontal size of the bounding box.
CC_STAT_HEIGHT  Python: cv.CC_STAT_HEIGHT	The vertical size of the bounding box.
CC_STAT_AREA  Python: cv.CC_STAT_AREA	The total area (in pixels) of the connected component.

ContourApproximationModes

enum cv::ContourApproximationModes

#include <opencv2/imgproc.hpp>

the contour approximation algorithm

Enumerator
CHAIN_APPROX_NONE  Python: cv.CHAIN_APPROX_NONE	stores absolutely all the contour points. That is, any 2 subsequent points (x1,y1) and (x2,y2) of the contour will be either horizontal, vertical or diagonal neighbors, that is, max(abs(x1-x2),abs(y2-y1))==1.
CHAIN_APPROX_SIMPLE  Python: cv.CHAIN_APPROX_SIMPLE	compresses horizontal, vertical, and diagonal segments and leaves only their end points. For example, an up-right rectangular contour is encoded with 4 points.
CHAIN_APPROX_TC89_L1  Python: cv.CHAIN_APPROX_TC89_L1	applies one of the flavors of the Teh-Chin chain approximation algorithm [266]
CHAIN_APPROX_TC89_KCOS  Python: cv.CHAIN_APPROX_TC89_KCOS	applies one of the flavors of the Teh-Chin chain approximation algorithm [266]

RectanglesIntersectTypes

enum cv::RectanglesIntersectTypes

#include <opencv2/imgproc.hpp>

types of intersection between rectangles

Enumerator
INTERSECT_NONE  Python: cv.INTERSECT_NONE	No intersection.
INTERSECT_PARTIAL  Python: cv.INTERSECT_PARTIAL	There is a partial intersection.
INTERSECT_FULL  Python: cv.INTERSECT_FULL	One of the rectangle is fully enclosed in the other.

RetrievalModes

enum cv::RetrievalModes

#include <opencv2/imgproc.hpp>

mode of the contour retrieval algorithm

Enumerator
RETR_EXTERNAL  Python: cv.RETR_EXTERNAL	retrieves only the extreme outer contours. It sets hierarchy[i][2]=hierarchy[i][3]=-1 for all the contours.
RETR_LIST  Python: cv.RETR_LIST	retrieves all of the contours without establishing any hierarchical relationships.
RETR_CCOMP  Python: cv.RETR_CCOMP	retrieves all of the contours and organizes them into a two-level hierarchy. At the top level, there are external boundaries of the components. At the second level, there are boundaries of the holes. If there is another contour inside a hole of a connected component, it is still put at the top level.
RETR_TREE  Python: cv.RETR_TREE	retrieves all of the contours and reconstructs a full hierarchy of nested contours.
RETR_FLOODFILL  Python: cv.RETR_FLOODFILL

ShapeMatchModes

enum cv::ShapeMatchModes

#include <opencv2/imgproc.hpp>

Shape matching methods.

\(A\) denotes object1, \(B\) denotes object2

\(\begin{array}{l} m^A_i = \mathrm{sign} (h^A_i) \cdot \log{h^A_i} \\ m^B_i = \mathrm{sign} (h^B_i) \cdot \log{h^B_i} \end{array}\)

and \(h^A_i, h^B_i\) are the Hu moments of \(A\) and \(B\) , respectively.

Enumerator
CONTOURS_MATCH_I1  Python: cv.CONTOURS_MATCH_I1	\[I_1(A,B) = \sum _{i=1...7} \left | \frac{1}{m^A_i} - \frac{1}{m^B_i} \right |\]
CONTOURS_MATCH_I2  Python: cv.CONTOURS_MATCH_I2	\[I_2(A,B) = \sum _{i=1...7} \left | m^A_i - m^B_i \right |\]
CONTOURS_MATCH_I3  Python: cv.CONTOURS_MATCH_I3	\[I_3(A,B) = \max _{i=1...7} \frac{ \left| m^A_i - m^B_i \right| }{ \left| m^A_i \right| }\]

Function Documentation

approxPolyDP()

void cv::approxPolyDP	(	InputArray	curve,
		OutputArray	approxCurve,
		double	epsilon,
		bool	closed
	)

Python:
	cv.approxPolyDP(	curve, epsilon, closed[, approxCurve]	) ->	approxCurve

#include <opencv2/imgproc.hpp>

Approximates a polygonal curve(s) with the specified precision.

The function cv::approxPolyDP approximates a curve or a polygon with another curve/polygon with less vertices so that the distance between them is less or equal to the specified precision. It uses the Douglas-Peucker algorithm http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm

Parameters

curve	Input vector of a 2D point stored in std::vector or Mat
approxCurve	Result of the approximation. The type should match the type of the input curve.
epsilon	Parameter specifying the approximation accuracy. This is the maximum distance between the original curve and its approximation.
closed	If true, the approximated curve is closed (its first and last vertices are connected). Otherwise, it is not closed.

approxPolyN()

void cv::approxPolyN	(	InputArray	curve,
		OutputArray	approxCurve,
		int	nsides,
		float	epsilon_percentage = -1.0,
		bool	ensure_convex = true
	)

Python:
	cv.approxPolyN(	curve, nsides[, approxCurve[, epsilon_percentage[, ensure_convex]]]	) ->	approxCurve

#include <opencv2/imgproc.hpp>

Approximates a polygon with a convex hull with a specified accuracy and number of sides.

The cv::approxPolyN function approximates a polygon with a convex hull so that the difference between the contour area of the original contour and the new polygon is minimal. It uses a greedy algorithm for contracting two vertices into one in such a way that the additional area is minimal. Straight lines formed by each edge of the convex contour are drawn and the areas of the resulting triangles are considered. Each vertex will lie either on the original contour or outside it.

The algorithm based on the paper [149] .

Parameters

curve	Input vector of a 2D points stored in std::vector or Mat, points must be float or integer.
approxCurve	Result of the approximation. The type is vector of a 2D point (Point2f or Point) in std::vector or Mat.
nsides	The parameter defines the number of sides of the result polygon.
epsilon_percentage	defines the percentage of the maximum of additional area. If it equals -1, it is not used. Otherwise algorighm stops if additional area is greater than contourArea(_curve) * percentage. If additional area exceeds the limit, algorithm returns as many vertices as there were at the moment the limit was exceeded.
ensure_convex	If it is true, algorithm creates a convex hull of input contour. Otherwise input vector should be convex.

arcLength()

double cv::arcLength	(	InputArray	curve,
		bool	closed
	)

Python:
	cv.arcLength(	curve, closed	) ->	retval

#include <opencv2/imgproc.hpp>

Calculates a contour perimeter or a curve length.

The function computes a curve length or a closed contour perimeter.

Parameters

curve	Input vector of 2D points, stored in std::vector or Mat.
closed	Flag indicating whether the curve is closed or not.

boundingRect()

Rect cv::boundingRect

(

InputArray

array

)

Python:
	cv.boundingRect(	array	) ->	retval

#include <opencv2/imgproc.hpp>

Calculates the up-right bounding rectangle of a point set or non-zero pixels of gray-scale image.

The function calculates and returns the minimal up-right bounding rectangle for the specified point set or non-zero pixels of gray-scale image.

Parameters

array

Input gray-scale image or 2D point set, stored in std::vector or Mat.

boxPoints()

void cv::boxPoints	(	RotatedRect	box,
		OutputArray	points
	)

Python:
	cv.boxPoints(	box[, points]	) ->	points

#include <opencv2/imgproc.hpp>

Finds the four vertices of a rotated rect. Useful to draw the rotated rectangle.

The function finds the four vertices of a rotated rectangle. This function is useful to draw the rectangle. In C++, instead of using this function, you can directly use RotatedRect::points method. Please visit the tutorial on Creating Bounding rotated boxes and ellipses for contours for more information.

Parameters

box	The input rotated rectangle. It may be the output of minAreaRect.
points	The output array of four vertices of rectangles.

connectedComponents() [1/2]

int cv::connectedComponents	(	InputArray	image,
		OutputArray	labels,
		int	connectivity,
		int	ltype,
		int	ccltype
	)

Python:
	cv.connectedComponents(	image[, labels[, connectivity[, ltype]]]	) ->	retval, labels
	cv.connectedComponentsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels]	) ->	retval, labels

#include <opencv2/imgproc.hpp>

computes the connected components labeled image of boolean image

image with 4 or 8 way connectivity - returns N, the total number of labels [0, N-1] where 0 represents the background label. ltype specifies the output label image type, an important consideration based on the total number of labels or alternatively the total number of pixels in the source image. ccltype specifies the connected components labeling algorithm to use, currently Bolelli (Spaghetti) [31], Grana (BBDT) [110] and Wu's (SAUF) [301] algorithms are supported, see the ConnectedComponentsAlgorithmsTypes for details. Note that SAUF algorithm forces a row major ordering of labels while Spaghetti and BBDT do not. This function uses parallel version of the algorithms if at least one allowed parallel framework is enabled and if the rows of the image are at least twice the number returned by getNumberOfCPUs.

Parameters

image	the 8-bit single-channel image to be labeled
labels	destination labeled image
connectivity	8 or 4 for 8-way or 4-way connectivity respectively
ltype	output image label type. Currently CV_32S and CV_16U are supported.
ccltype	connected components algorithm type (see the ConnectedComponentsAlgorithmsTypes).

connectedComponents() [2/2]

int cv::connectedComponents	(	InputArray	image,
		OutputArray	labels,
		int	connectivity = 8,
		int	ltype = CV_32S
	)

Python:
	cv.connectedComponents(	image[, labels[, connectivity[, ltype]]]	) ->	retval, labels
	cv.connectedComponentsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels]	) ->	retval, labels

#include <opencv2/imgproc.hpp>

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Parameters

image	the 8-bit single-channel image to be labeled
labels	destination labeled image
connectivity	8 or 4 for 8-way or 4-way connectivity respectively
ltype	output image label type. Currently CV_32S and CV_16U are supported.

connectedComponentsWithStats() [1/2]

int cv::connectedComponentsWithStats	(	InputArray	image,
		OutputArray	labels,
		OutputArray	stats,
		OutputArray	centroids,
		int	connectivity,
		int	ltype,
		int	ccltype
	)

Python:
	cv.connectedComponentsWithStats(	image[, labels[, stats[, centroids[, connectivity[, ltype]]]]]	) ->	retval, labels, stats, centroids
	cv.connectedComponentsWithStatsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels[, stats[, centroids]]]	) ->	retval, labels, stats, centroids

#include <opencv2/imgproc.hpp>

computes the connected components labeled image of boolean image and also produces a statistics output for each label

image with 4 or 8 way connectivity - returns N, the total number of labels [0, N-1] where 0 represents the background label. ltype specifies the output label image type, an important consideration based on the total number of labels or alternatively the total number of pixels in the source image. ccltype specifies the connected components labeling algorithm to use, currently Bolelli (Spaghetti) [31], Grana (BBDT) [110] and Wu's (SAUF) [301] algorithms are supported, see the ConnectedComponentsAlgorithmsTypes for details. Note that SAUF algorithm forces a row major ordering of labels while Spaghetti and BBDT do not. This function uses parallel version of the algorithms (statistics included) if at least one allowed parallel framework is enabled and if the rows of the image are at least twice the number returned by getNumberOfCPUs.

Parameters

image	the 8-bit single-channel image to be labeled
labels	destination labeled image
stats	statistics output for each label, including the background label. Statistics are accessed via stats(label, COLUMN) where COLUMN is one of ConnectedComponentsTypes, selecting the statistic. The data type is CV_32S.
centroids	centroid output for each label, including the background label. Centroids are accessed via centroids(label, 0) for x and centroids(label, 1) for y. The data type CV_64F.
connectivity	8 or 4 for 8-way or 4-way connectivity respectively
ltype	output image label type. Currently CV_32S and CV_16U are supported.
ccltype	connected components algorithm type (see ConnectedComponentsAlgorithmsTypes).

connectedComponentsWithStats() [2/2]

int cv::connectedComponentsWithStats	(	InputArray	image,
		OutputArray	labels,
		OutputArray	stats,
		OutputArray	centroids,
		int	connectivity = 8,
		int	ltype = CV_32S
	)

Python:
	cv.connectedComponentsWithStats(	image[, labels[, stats[, centroids[, connectivity[, ltype]]]]]	) ->	retval, labels, stats, centroids
	cv.connectedComponentsWithStatsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels[, stats[, centroids]]]	) ->	retval, labels, stats, centroids

#include <opencv2/imgproc.hpp>

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Parameters

image	the 8-bit single-channel image to be labeled
labels	destination labeled image
stats	statistics output for each label, including the background label. Statistics are accessed via stats(label, COLUMN) where COLUMN is one of ConnectedComponentsTypes, selecting the statistic. The data type is CV_32S.
centroids	centroid output for each label, including the background label. Centroids are accessed via centroids(label, 0) for x and centroids(label, 1) for y. The data type CV_64F.
connectivity	8 or 4 for 8-way or 4-way connectivity respectively
ltype	output image label type. Currently CV_32S and CV_16U are supported.

contourArea()

double cv::contourArea	(	InputArray	contour,
		bool	oriented = false
	)

Python:
	cv.contourArea(	contour[, oriented]	) ->	retval

#include <opencv2/imgproc.hpp>

Calculates a contour area.

The function computes a contour area. Similarly to moments , the area is computed using the Green formula. Thus, the returned area and the number of non-zero pixels, if you draw the contour using drawContours or fillPoly , can be different. Also, the function will most certainly give a wrong results for contours with self-intersections.

Example:

vector<Point> contour;
contour.push_back(Point2f(0, 0));
contour.push_back(Point2f(10, 0));
contour.push_back(Point2f(10, 10));
contour.push_back(Point2f(5, 4));
 
double area0 = contourArea(contour);
vector<Point> approx;
approxPolyDP(contour, approx, 5, true);
double area1 = contourArea(approx);
 
cout << "area0 =" << area0 << endl <<
        "area1 =" << area1 << endl <<
        "approx poly vertices" << approx.size() << endl;

Parameters

contour	Input vector of 2D points (contour vertices), stored in std::vector or Mat.
oriented	Oriented area flag. If it is true, the function returns a signed area value, depending on the contour orientation (clockwise or counter-clockwise). Using this feature you can determine orientation of a contour by taking the sign of an area. By default, the parameter is false, which means that the absolute value is returned.

convexHull()

void cv::convexHull	(	InputArray	points,
		OutputArray	hull,
		bool	clockwise = false,
		bool	returnPoints = true
	)

Python:
	cv.convexHull(	points[, hull[, clockwise[, returnPoints]]]	) ->	hull

#include <opencv2/imgproc.hpp>

Finds the convex hull of a point set.

The function cv::convexHull finds the convex hull of a 2D point set using the Sklansky's algorithm [247] that has O(N logN) complexity in the current implementation.

Parameters

points	Input 2D point set, stored in std::vector or Mat.
hull	Output convex hull. It is either an integer vector of indices or vector of points. In the first case, the hull elements are 0-based indices of the convex hull points in the original array (since the set of convex hull points is a subset of the original point set). In the second case, hull elements are the convex hull points themselves.
clockwise	Orientation flag. If it is true, the output convex hull is oriented clockwise. Otherwise, it is oriented counter-clockwise. The assumed coordinate system has its X axis pointing to the right, and its Y axis pointing upwards.
returnPoints	Operation flag. In case of a matrix, when the flag is true, the function returns convex hull points. Otherwise, it returns indices of the convex hull points. When the output array is std::vector, the flag is ignored, and the output depends on the type of the vector: std::vector<int> implies returnPoints=false, std::vector<Point> implies returnPoints=true.

Note

points and hull should be different arrays, inplace processing isn't supported.

Check the corresponding tutorial for more details.

useful links:

https://www.learnopencv.com/convex-hull-using-opencv-in-python-and-c/

convexityDefects()

void cv::convexityDefects	(	InputArray	contour,
		InputArray	convexhull,
		OutputArray	convexityDefects
	)

Python:
	cv.convexityDefects(	contour, convexhull[, convexityDefects]	) ->	convexityDefects

#include <opencv2/imgproc.hpp>

Finds the convexity defects of a contour.

The figure below displays convexity defects of a hand contour:

image

Parameters

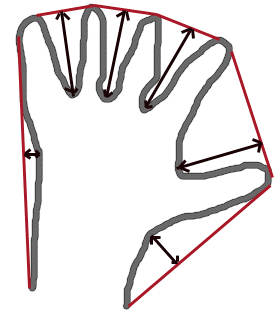
contour	Input contour.
convexhull	Convex hull obtained using convexHull that should contain indices of the contour points that make the hull.
convexityDefects	The output vector of convexity defects. In C++ and the new Python/Java interface each convexity defect is represented as 4-element integer vector (a.k.a. Vec4i): (start_index, end_index, farthest_pt_index, fixpt_depth), where indices are 0-based indices in the original contour of the convexity defect beginning, end and the farthest point, and fixpt_depth is fixed-point approximation (with 8 fractional bits) of the distance between the farthest contour point and the hull. That is, to get the floating-point value of the depth will be fixpt_depth/256.0.

createGeneralizedHoughBallard()

Ptr< GeneralizedHoughBallard > cv::createGeneralizedHoughBallard

(

)

Python:
	cv.createGeneralizedHoughBallard(		) ->	retval

#include <opencv2/imgproc.hpp>

Creates a smart pointer to a cv::GeneralizedHoughBallard class and initializes it.

createGeneralizedHoughGuil()

Ptr< GeneralizedHoughGuil > cv::createGeneralizedHoughGuil

(

)

Python:
	cv.createGeneralizedHoughGuil(		) ->	retval

#include <opencv2/imgproc.hpp>

Creates a smart pointer to a cv::GeneralizedHoughGuil class and initializes it.

findContours() [1/2]

void cv::findContours	(	InputArray	image,
		OutputArrayOfArrays	contours,
		int	mode,
		int	method,
		Point	offset = Point()
	)

Python:
	cv.findContours(	image, mode, method[, contours[, hierarchy[, offset]]]	) ->	contours, hierarchy

#include <opencv2/imgproc.hpp>

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

findContours() [2/2]

void cv::findContours	(	InputArray	image,
		OutputArrayOfArrays	contours,
		OutputArray	hierarchy,
		int	mode,
		int	method,
		Point	offset = Point()
	)

Python:
	cv.findContours(	image, mode, method[, contours[, hierarchy[, offset]]]	) ->	contours, hierarchy

#include <opencv2/imgproc.hpp>

Finds contours in a binary image.

The function retrieves contours from the binary image using the algorithm [258] . The contours are a useful tool for shape analysis and object detection and recognition. See squares.cpp in the OpenCV sample directory.

Note

Since opencv 3.2 source image is not modified by this function.

Parameters

image	Source, an 8-bit single-channel image. Non-zero pixels are treated as 1's. Zero pixels remain 0's, so the image is treated as binary . You can use compare, inRange, threshold , adaptiveThreshold, Canny, and others to create a binary image out of a grayscale or color one. If mode equals to RETR_CCOMP or RETR_FLOODFILL, the input can also be a 32-bit integer image of labels (CV_32SC1).
contours	Detected contours. Each contour is stored as a vector of points (e.g. std::vector<std::vector<cv::Point> >).
hierarchy	Optional output vector (e.g. std::vector<cv::Vec4i>), containing information about the image topology. It has as many elements as the number of contours. For each i-th contour contours[i], the elements hierarchy[i][0] , hierarchy[i][1] , hierarchy[i][2] , and hierarchy[i][3] are set to 0-based indices in contours of the next and previous contours at the same hierarchical level, the first child contour and the parent contour, respectively. If for the contour i there are no next, previous, parent, or nested contours, the corresponding elements of hierarchy[i] will be negative.

Note

In Python, hierarchy is nested inside a top level array. Use hierarchy[0][i] to access hierarchical elements of i-th contour.

Parameters

mode	Contour retrieval mode, see RetrievalModes
method	Contour approximation method, see ContourApproximationModes
offset	Optional offset by which every contour point is shifted. This is useful if the contours are extracted from the image ROI and then they should be analyzed in the whole image context.

findContoursLinkRuns() [1/2]

void cv::findContoursLinkRuns	(	InputArray	image,
		OutputArrayOfArrays	contours
	)

Python:
	cv.findContoursLinkRuns(	image[, contours[, hierarchy]]	) ->	contours, hierarchy
	cv.findContoursLinkRuns(	image[, contours]	) ->	contours

#include <opencv2/imgproc.hpp>

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

findContoursLinkRuns() [2/2]

void cv::findContoursLinkRuns	(	InputArray	image,
		OutputArrayOfArrays	contours,
		OutputArray	hierarchy
	)

Python:
	cv.findContoursLinkRuns(	image[, contours[, hierarchy]]	) ->	contours, hierarchy
	cv.findContoursLinkRuns(	image[, contours]	) ->	contours

#include <opencv2/imgproc.hpp>

Find contours using link runs algorithm.

This function implements an algorithm different from cv::findContours:

• doesn't allocate temporary image internally, thus it has reduced memory consumption
• supports CV_8UC1 images only
• outputs 2-level hierarhy only (RETR_CCOMP mode)
• doesn't support approximation change other than CHAIN_APPROX_SIMPLE In all other aspects this function is compatible with cv::findContours.

fitEllipse()

RotatedRect cv::fitEllipse

(

InputArray

points

)

Python:
	cv.fitEllipse(	points	) ->	retval

#include <opencv2/imgproc.hpp>

Fits an ellipse around a set of 2D points.

The function calculates the ellipse that fits (in a least-squares sense) a set of 2D points best of all. It returns the rotated rectangle in which the ellipse is inscribed. The first algorithm described by [92] is used. Developer should keep in mind that it is possible that the returned ellipse/rotatedRect data contains negative indices, due to the data points being close to the border of the containing Mat element.

Parameters

points

Input 2D point set, stored in std::vector<> or Mat

fitEllipseAMS()

RotatedRect cv::fitEllipseAMS

(

InputArray

points

)

Python:
	cv.fitEllipseAMS(	points	) ->	retval

#include <opencv2/imgproc.hpp>

Fits an ellipse around a set of 2D points.

The function calculates the ellipse that fits a set of 2D points. It returns the rotated rectangle in which the ellipse is inscribed. The Approximate Mean Square (AMS) proposed by [265] is used.

For an ellipse, this basis set is \( \chi= \left(x^2, x y, y^2, x, y, 1\right) \), which is a set of six free coefficients \( A^T=\left\{A_{\text{xx}},A_{\text{xy}},A_{\text{yy}},A_x,A_y,A_0\right\} \). However, to specify an ellipse, all that is needed is five numbers; the major and minor axes lengths \( (a,b) \), the position \( (x_0,y_0) \), and the orientation \( \theta \). This is because the basis set includes lines, quadratics, parabolic and hyperbolic functions as well as elliptical functions as possible fits. If the fit is found to be a parabolic or hyperbolic function then the standard fitEllipse method is used. The AMS method restricts the fit to parabolic, hyperbolic and elliptical curves by imposing the condition that \( A^T ( D_x^T D_x + D_y^T D_y) A = 1 \) where the matrices \( Dx \) and \( Dy \) are the partial derivatives of the design matrix \( D \) with respect to x and y. The matrices are formed row by row applying the following to each of the points in the set:

\begin{align*} D(i,:)&=\left\{x_i^2, x_i y_i, y_i^2, x_i, y_i, 1\right\} & D_x(i,:)&=\left\{2 x_i,y_i,0,1,0,0\right\} & D_y(i,:)&=\left\{0,x_i,2 y_i,0,1,0\right\} \end{align*}

The AMS method minimizes the cost function

\begin{equation*} \epsilon ^2=\frac{ A^T D^T D A }{ A^T (D_x^T D_x + D_y^T D_y) A^T } \end{equation*}

The minimum cost is found by solving the generalized eigenvalue problem.

\begin{equation*} D^T D A = \lambda \left( D_x^T D_x + D_y^T D_y\right) A \end{equation*}

Parameters

points

Input 2D point set, stored in std::vector<> or Mat

fitEllipseDirect()

RotatedRect cv::fitEllipseDirect

(

InputArray

points

)

Python:
	cv.fitEllipseDirect(	points	) ->	retval

#include <opencv2/imgproc.hpp>

Fits an ellipse around a set of 2D points.

The function calculates the ellipse that fits a set of 2D points. It returns the rotated rectangle in which the ellipse is inscribed. The Direct least square (Direct) method by [93] is used.

For an ellipse, this basis set is \( \chi= \left(x^2, x y, y^2, x, y, 1\right) \), which is a set of six free coefficients \( A^T=\left\{A_{\text{xx}},A_{\text{xy}},A_{\text{yy}},A_x,A_y,A_0\right\} \). However, to specify an ellipse, all that is needed is five numbers; the major and minor axes lengths \( (a,b) \), the position \( (x_0,y_0) \), and the orientation \( \theta \). This is because the basis set includes lines, quadratics, parabolic and hyperbolic functions as well as elliptical functions as possible fits. The Direct method confines the fit to ellipses by ensuring that \( 4 A_{xx} A_{yy}- A_{xy}^2 > 0 \). The condition imposed is that \( 4 A_{xx} A_{yy}- A_{xy}^2=1 \) which satisfies the inequality and as the coefficients can be arbitrarily scaled is not overly restrictive.

\begin{equation*} \epsilon ^2= A^T D^T D A \quad \text{with} \quad A^T C A =1 \quad \text{and} \quad C=\left(\begin{matrix} 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix} \right) \end{equation*}

The minimum cost is found by solving the generalized eigenvalue problem.

\begin{equation*} D^T D A = \lambda \left( C\right) A \end{equation*}

The system produces only one positive eigenvalue \( \lambda\) which is chosen as the solution with its eigenvector \(\mathbf{u}\). These are used to find the coefficients

\begin{equation*} A = \sqrt{\frac{1}{\mathbf{u}^T C \mathbf{u}}} \mathbf{u} \end{equation*}

The scaling factor guarantees that \(A^T C A =1\).

Parameters

points

Input 2D point set, stored in std::vector<> or Mat

fitLine()

void cv::fitLine	(	InputArray	points,
		OutputArray	line,
		int	distType,
		double	param,
		double	reps,
		double	aeps
	)

Python:
	cv.fitLine(	points, distType, param, reps, aeps[, line]	) ->	line

#include <opencv2/imgproc.hpp>

Fits a line to a 2D or 3D point set.

The function fitLine fits a line to a 2D or 3D point set by minimizing \(\sum_i \rho(r_i)\) where \(r_i\) is a distance between the \(i^{th}\) point, the line and \(\rho(r)\) is a distance function, one of the following:

• DIST_L2

  \[\rho (r) = r^2/2 \quad \text{(the simplest and the fastest least-squares method)}\]

• DIST_L1

  \[\rho (r) = r\]

• DIST_L12

  \[\rho (r) = 2 \cdot ( \sqrt{1 + \frac{r^2}{2}} - 1)\]

• DIST_FAIR

  \[\rho \left (r \right ) = C^2 \cdot \left ( \frac{r}{C} - \log{\left(1 + \frac{r}{C}\right)} \right ) \quad \text{where} \quad C=1.3998\]

• DIST_WELSCH

  \[\rho \left (r \right ) = \frac{C^2}{2} \cdot \left ( 1 - \exp{\left(-\left(\frac{r}{C}\right)^2\right)} \right ) \quad \text{where} \quad C=2.9846\]

• DIST_HUBER

  \[\rho (r) = \fork{r^2/2}{if \(r < C\)}{C \cdot (r-C/2)}{otherwise} \quad \text{where} \quad C=1.345\]

The algorithm is based on the M-estimator ( http://en.wikipedia.org/wiki/M-estimator ) technique that iteratively fits the line using the weighted least-squares algorithm. After each iteration the weights \(w_i\) are adjusted to be inversely proportional to \(\rho(r_i)\) .

Parameters

points	Input vector of 2D or 3D points, stored in std::vector<> or Mat.
line	Output line parameters. In case of 2D fitting, it should be a vector of 4 elements (like Vec4f) - (vx, vy, x0, y0), where (vx, vy) is a normalized vector collinear to the line and (x0, y0) is a point on the line. In case of 3D fitting, it should be a vector of 6 elements (like Vec6f) - (vx, vy, vz, x0, y0, z0), where (vx, vy, vz) is a normalized vector collinear to the line and (x0, y0, z0) is a point on the line.
distType	Distance used by the M-estimator, see DistanceTypes
param	Numerical parameter ( C ) for some types of distances. If it is 0, an optimal value is chosen.
reps	Sufficient accuracy for the radius (distance between the coordinate origin and the line).
aeps	Sufficient accuracy for the angle. 0.01 would be a good default value for reps and aeps.

HuMoments() [1/2]

void cv::HuMoments	(	const Moments &	m,
		OutputArray	hu
	)

Python:
	cv.HuMoments(	m[, hu]	) ->	hu

#include <opencv2/imgproc.hpp>

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

HuMoments() [2/2]

void cv::HuMoments	(	const Moments &	moments,
		double	hu[7]
	)

Python:
	cv.HuMoments(	m[, hu]	) ->	hu

#include <opencv2/imgproc.hpp>

Calculates seven Hu invariants.

The function calculates seven Hu invariants (introduced in [131]; see also http://en.wikipedia.org/wiki/Image_moment) defined as:

\[\begin{array}{l} hu[0]= \eta _{20}+ \eta _{02} \\ hu[1]=( \eta _{20}- \eta _{02})^{2}+4 \eta _{11}^{2} \\ hu[2]=( \eta _{30}-3 \eta _{12})^{2}+ (3 \eta _{21}- \eta _{03})^{2} \\ hu[3]=( \eta _{30}+ \eta _{12})^{2}+ ( \eta _{21}+ \eta _{03})^{2} \\ hu[4]=( \eta _{30}-3 \eta _{12})( \eta _{30}+ \eta _{12})[( \eta _{30}+ \eta _{12})^{2}-3( \eta _{21}+ \eta _{03})^{2}]+(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ hu[5]=( \eta _{20}- \eta _{02})[( \eta _{30}+ \eta _{12})^{2}- ( \eta _{21}+ \eta _{03})^{2}]+4 \eta _{11}( \eta _{30}+ \eta _{12})( \eta _{21}+ \eta _{03}) \\ hu[6]=(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}]-( \eta _{30}-3 \eta _{12})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ \end{array}\]

where \(\eta_{ji}\) stands for \(\texttt{Moments::nu}_{ji}\) .

These values are proved to be invariants to the image scale, rotation, and reflection except the seventh one, whose sign is changed by reflection. This invariance is proved with the assumption of infinite image resolution. In case of raster images, the computed Hu invariants for the original and transformed images are a bit different.

Parameters

moments	Input moments computed with moments .
hu	Output Hu invariants.

See also

matchShapes

intersectConvexConvex()

float cv::intersectConvexConvex	(	InputArray	p1,
		InputArray	p2,
		OutputArray	p12,
		bool	handleNested = true
	)

Python:
	cv.intersectConvexConvex(	p1, p2[, p12[, handleNested]]	) ->	retval, p12

#include <opencv2/imgproc.hpp>

Finds intersection of two convex polygons.

Parameters

p1	First polygon
p2	Second polygon
p12	Output polygon describing the intersecting area
handleNested	When true, an intersection is found if one of the polygons is fully enclosed in the other. When false, no intersection is found. If the polygons share a side or the vertex of one polygon lies on an edge of the other, they are not considered nested and an intersection will be found regardless of the value of handleNested.

Returns

Area of intersecting polygon. May be negative, if algorithm has not converged, e.g. non-convex input.

Note

intersectConvexConvex doesn't confirm that both polygons are convex and will return invalid results if they aren't.

isContourConvex()

bool cv::isContourConvex

(

InputArray

contour

)

Python:
	cv.isContourConvex(	contour	) ->	retval

#include <opencv2/imgproc.hpp>

Tests a contour convexity.

The function tests whether the input contour is convex or not. The contour must be simple, that is, without self-intersections. Otherwise, the function output is undefined.

Parameters

contour

Input vector of 2D points, stored in std::vector<> or Mat

matchShapes()

double cv::matchShapes	(	InputArray	contour1,
		InputArray	contour2,
		int	method,
		double	parameter
	)

Python:
	cv.matchShapes(	contour1, contour2, method, parameter	) ->	retval

#include <opencv2/imgproc.hpp>

Compares two shapes.

The function compares two shapes. All three implemented methods use the Hu invariants (see HuMoments)

Parameters

contour1	First contour or grayscale image.
contour2	Second contour or grayscale image.
method	Comparison method, see ShapeMatchModes
parameter	Method-specific parameter (not supported now).

minAreaRect()

RotatedRect cv::minAreaRect

(

InputArray

points

)

Python:
	cv.minAreaRect(	points	) ->	retval

#include <opencv2/imgproc.hpp>

Finds a rotated rectangle of the minimum area enclosing the input 2D point set.

The function calculates and returns the minimum-area bounding rectangle (possibly rotated) for a specified point set. Developer should keep in mind that the returned RotatedRect can contain negative indices when data is close to the containing Mat element boundary.

Parameters

points

Input vector of 2D points, stored in std::vector<> or Mat

minEnclosingCircle()

void cv::minEnclosingCircle	(	InputArray	points,
		Point2f &	center,
		float &	radius
	)

Python:
	cv.minEnclosingCircle(	points	) ->	center, radius

#include <opencv2/imgproc.hpp>

Finds a circle of the minimum area enclosing a 2D point set.

The function finds the minimal enclosing circle of a 2D point set using an iterative algorithm.

Parameters

points	Input vector of 2D points, stored in std::vector<> or Mat
center	Output center of the circle.
radius	Output radius of the circle.

minEnclosingTriangle()

double cv::minEnclosingTriangle	(	InputArray	points,
		OutputArray	triangle
	)

Python:
	cv.minEnclosingTriangle(	points[, triangle]	) ->	retval, triangle

#include <opencv2/imgproc.hpp>

Finds a triangle of minimum area enclosing a 2D point set and returns its area.

The function finds a triangle of minimum area enclosing the given set of 2D points and returns its area. The output for a given 2D point set is shown in the image below. 2D points are depicted in red* and the enclosing triangle in yellow.

Sample output of the minimum enclosing triangle function

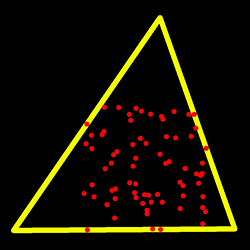
The implementation of the algorithm is based on O'Rourke's [211] and Klee and Laskowski's [148] papers. O'Rourke provides a \(\theta(n)\) algorithm for finding the minimal enclosing triangle of a 2D convex polygon with n vertices. Since the minEnclosingTriangle function takes a 2D point set as input an additional preprocessing step of computing the convex hull of the 2D point set is required. The complexity of the convexHull function is \(O(n log(n))\) which is higher than \(\theta(n)\). Thus the overall complexity of the function is \(O(n log(n))\).

Parameters

points	Input vector of 2D points with depth CV_32S or CV_32F, stored in std::vector<> or Mat
triangle	Output vector of three 2D points defining the vertices of the triangle. The depth of the OutputArray must be CV_32F.

moments()

Moments cv::moments	(	InputArray	array,
		bool	binaryImage = false
	)

Python:
	cv.moments(	array[, binaryImage]	) ->	retval

#include <opencv2/imgproc.hpp>

Calculates all of the moments up to the third order of a polygon or rasterized shape.

The function computes moments, up to the 3rd order, of a vector shape or a rasterized shape. The results are returned in the structure cv::Moments.

Parameters

array	Single chanel raster image (CV_8U, CV_16U, CV_16S, CV_32F, CV_64F) or an array ( \(1 \times N\) or \(N \times 1\) ) of 2D points (Point or Point2f).
binaryImage	If it is true, all non-zero image pixels are treated as 1's. The parameter is used for images only.

Returns

moments.

Note

Only applicable to contour moments calculations from Python bindings: Note that the numpy type for the input array should be either np.int32 or np.float32.

See also

contourArea, arcLength

pointPolygonTest()

double cv::pointPolygonTest	(	InputArray	contour,
		Point2f	pt,
		bool	measureDist
	)

Python:
	cv.pointPolygonTest(	contour, pt, measureDist	) ->	retval

#include <opencv2/imgproc.hpp>

Performs a point-in-contour test.

The function determines whether the point is inside a contour, outside, or lies on an edge (or coincides with a vertex). It returns positive (inside), negative (outside), or zero (on an edge) value, correspondingly. When measureDist=false , the return value is +1, -1, and 0, respectively. Otherwise, the return value is a signed distance between the point and the nearest contour edge.

See below a sample output of the function where each image pixel is tested against the contour:

sample output

Parameters

contour	Input contour.
pt	Point tested against the contour.
measureDist	If true, the function estimates the signed distance from the point to the nearest contour edge. Otherwise, the function only checks if the point is inside a contour or not.

rotatedRectangleIntersection()

int cv::rotatedRectangleIntersection	(	const RotatedRect &	rect1,
		const RotatedRect &	rect2,
		OutputArray	intersectingRegion
	)

Python:
	cv.rotatedRectangleIntersection(	rect1, rect2[, intersectingRegion]	) ->	retval, intersectingRegion

#include <opencv2/imgproc.hpp>

Finds out if there is any intersection between two rotated rectangles.

If there is then the vertices of the intersecting region are returned as well.

Below are some examples of intersection configurations. The hatched pattern indicates the intersecting region and the red vertices are returned by the function.

intersection examples

Parameters

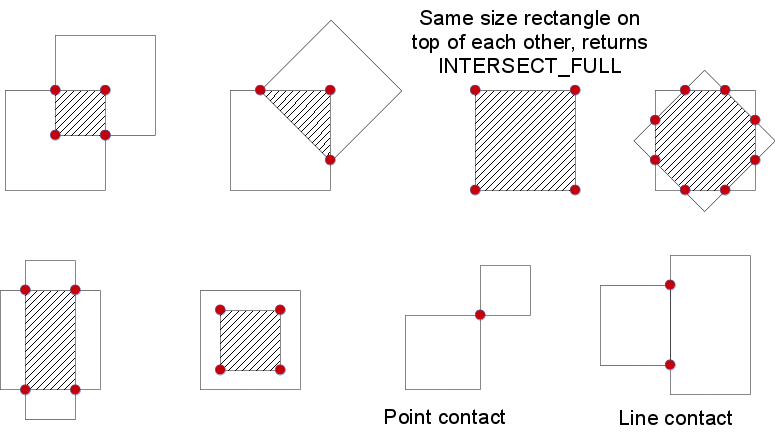
rect1	First rectangle
rect2	Second rectangle
intersectingRegion	The output array of the vertices of the intersecting region. It returns at most 8 vertices. Stored as std::vector<cv::Point2f> or cv::Mat as Mx1 of type CV_32FC2.

Returns

One of RectanglesIntersectTypes