|
OpenCV 4.13.0-dev
Open Source Computer Vision
|
 |
OpenCV 4.13.0-dev
Open Source Computer Vision
|
Prev Tutorial: Object detection with Generalized Ballard and Guil Hough Transform
Next Tutorial: Affine Transformations
| Original author | Ana Huamán |
| Compatibility | OpenCV >= 3.0 |
In this tutorial you will learn how to:
a. Use the OpenCV function cv::remap to implement simple remapping routines.
We can express the remap for every pixel location \((x,y)\) as:
\[g(x,y) = f ( h(x,y) )\]
where \(g()\) is the remapped image, \(f()\) the source image and \(h(x,y)\) is the mapping function that operates on \((x,y)\).
Let's think in a quick example. Imagine that we have an image \(I\) and, say, we want to do a remap such that:
\[h(x,y) = (I.cols - x, y )\]
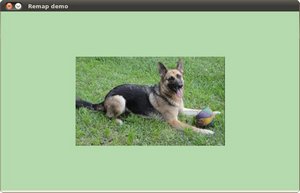
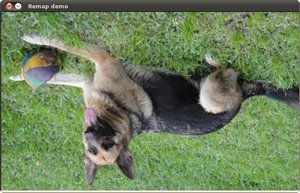
What would happen? It is easily seen that the image would flip in the \(x\) direction. For instance, consider the input image:

observe how the red circle changes positions with respect to \(x\) (considering \(x\) the horizontal direction):

Load an image:
Create the destination image and the two mapping matrices (for x and y )
Create a window to display results
Establish a loop. Each 1000 ms we update our mapping matrices (mat_x and mat_y) and apply them to our source image:
The function that applies the remapping is cv::remap . We give the following arguments:
How do we update our mapping matrices mat_x and mat_y? Go on reading:
\[h(i,j) = ( 2 \times i - src.cols/2 + 0.5, 2 \times j - src.rows/2 + 0.5)\]
for all pairs \((i,j)\) such that: \(\dfrac{src.cols}{4}<i<\dfrac{3 \cdot src.cols}{4}\) and \(\dfrac{src.rows}{4}<j<\dfrac{3 \cdot src.rows}{4}\)This is expressed in the following snippet. Here, map_x represents the first coordinate of h(i,j) and map_y the second coordinate.