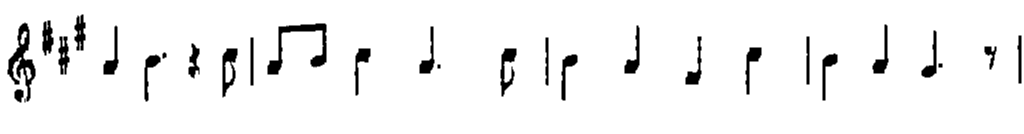Extract horizontal and vertical lines by using morphological operations

Table of Contents

• Goal
• Theory
  • Morphology Operations
  • Structuring Elements
• Code
• Explanation / Result
  • Load Image
  • Grayscale
  • Grayscale to Binary image
  • Output images
  • Structure elements
  • Refine edges / Result

Prev Tutorial: Hit-or-Miss
Next Tutorial: Image Pyramids

Original author	Theodore Tsesmelis
Compatibility	OpenCV >= 3.0

Goal

In this tutorial you will learn how to:

• Apply two very common morphology operators (i.e. Dilation and Erosion), with the creation of custom kernels, in order to extract straight lines on the horizontal and vertical axes. For this purpose, you will use the following OpenCV functions:

  • erode()
  • dilate()
  • getStructuringElement()

  in an example where your goal will be to extract the music notes from a music sheet.

Theory

Morphology Operations

Morphology is a set of image processing operations that process images based on predefined structuring elements known also as kernels. The value of each pixel in the output image is based on a comparison of the corresponding pixel in the input image with its neighbors. By choosing the size and shape of the kernel, you can construct a morphological operation that is sensitive to specific shapes regarding the input image.

Two of the most basic morphological operations are dilation and erosion. Dilation adds pixels to the boundaries of the object in an image, while erosion does exactly the opposite. The amount of pixels added or removed, respectively depends on the size and shape of the structuring element used to process the image. In general the rules followed from these two operations have as follows:

• Dilation: The value of the output pixel is the maximum value of all the pixels that fall within the structuring element's size and shape. For example in a binary image, if any of the pixels of the input image falling within the range of the kernel is set to the value 1, the corresponding pixel of the output image will be set to 1 as well. The latter applies to any type of image (e.g. grayscale, bgr, etc).

Dilation on a Binary Image

Dilation on a Grayscale Image

• Erosion: The vice versa applies for the erosion operation. The value of the output pixel is the minimum value of all the pixels that fall within the structuring element's size and shape. Look the at the example figures below:

Erosion on a Binary Image

Erosion on a Grayscale Image

Structuring Elements

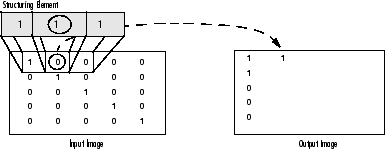
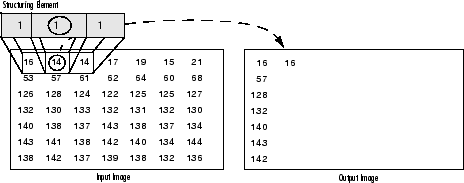
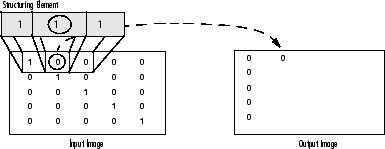
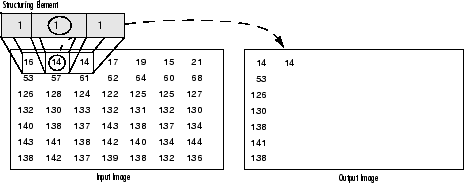
As it can be seen above and in general in any morphological operation the structuring element used to probe the input image, is the most important part.

A structuring element is a matrix consisting of only 0's and 1's that can have any arbitrary shape and size. Typically are much smaller than the image being processed, while the pixels with values of 1 define the neighborhood. The center pixel of the structuring element, called the origin, identifies the pixel of interest – the pixel being processed.

For example, the following illustrates a diamond-shaped structuring element of 7x7 size.

A Diamond-Shaped Structuring Element and its Origin

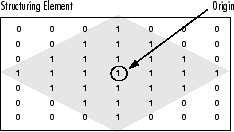
A structuring element can have many common shapes, such as lines, diamonds, disks, periodic lines, and circles and sizes. You typically choose a structuring element the same size and shape as the objects you want to process/extract in the input image. For example, to find lines in an image, create a linear structuring element as you will see later.

Code

This tutorial code's is shown lines below.

C++

You can also download it from here.

 
#include <opencv2/core.hpp>
#include <opencv2/imgproc.hpp>
#include <opencv2/highgui.hpp>
#include <iostream>
 
void show_wait_destroy(const char* winname, cv::Mat img);
 
using namespace std;
using namespace cv;
 
int main(int argc, char** argv)
{
    CommandLineParser parser(argc, argv, "{@input | notes.png | input image}");
    Mat src = imread( samples::findFile( parser.get<String>("@input") ), IMREAD_COLOR);
    if (src.empty())
    {
        cout << "Could not open or find the image!\n" << endl;
        cout << "Usage: " << argv[0] << " <Input image>" << endl;
        return -1;
    }
 
    // Show source image
    imshow("src", src);
 
    // Transform source image to gray if it is not already
    Mat gray;
 
    if (src.channels() == 3)
    {
        cvtColor(src, gray, COLOR_BGR2GRAY);
    }
    else
    {
        gray = src;
    }
 
    // Show gray image
    show_wait_destroy("gray", gray);
 
    // Apply adaptiveThreshold at the bitwise_not of gray, notice the ~ symbol
    Mat bw;
    adaptiveThreshold(~gray, bw, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 15, -2);
 
    // Show binary image
    show_wait_destroy("binary", bw);
 
    // Create the images that will use to extract the horizontal and vertical lines
    Mat horizontal = bw.clone();
    Mat vertical = bw.clone();
 
    // Specify size on horizontal axis
    int horizontal_size = horizontal.cols / 30;
 
    // Create structure element for extracting horizontal lines through morphology operations
    Mat horizontalStructure = getStructuringElement(MORPH_RECT, Size(horizontal_size, 1));
 
    // Apply morphology operations
    erode(horizontal, horizontal, horizontalStructure, Point(-1, -1));
    dilate(horizontal, horizontal, horizontalStructure, Point(-1, -1));
 
    // Show extracted horizontal lines
    show_wait_destroy("horizontal", horizontal);
 
    // Specify size on vertical axis
    int vertical_size = vertical.rows / 30;
 
    // Create structure element for extracting vertical lines through morphology operations
    Mat verticalStructure = getStructuringElement(MORPH_RECT, Size(1, vertical_size));
 
    // Apply morphology operations
    erode(vertical, vertical, verticalStructure, Point(-1, -1));
    dilate(vertical, vertical, verticalStructure, Point(-1, -1));
 
    // Show extracted vertical lines
    show_wait_destroy("vertical", vertical);
 
    // Inverse vertical image
    bitwise_not(vertical, vertical);
    show_wait_destroy("vertical_bit", vertical);
 
    // Extract edges and smooth image according to the logic
    // 1. extract edges
    // 2. dilate(edges)
    // 3. src.copyTo(smooth)
    // 4. blur smooth img
    // 5. smooth.copyTo(src, edges)
 
    // Step 1
    Mat edges;
    adaptiveThreshold(vertical, edges, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 3, -2);
    show_wait_destroy("edges", edges);
 
    // Step 2
    Mat kernel = Mat::ones(2, 2, CV_8UC1);
    dilate(edges, edges, kernel);
    show_wait_destroy("dilate", edges);
 
    // Step 3
    Mat smooth;
    vertical.copyTo(smooth);
 
    // Step 4
    blur(smooth, smooth, Size(2, 2));
 
    // Step 5
    smooth.copyTo(vertical, edges);
 
    // Show final result
    show_wait_destroy("smooth - final", vertical);
 
    return 0;
}
 
void show_wait_destroy(const char* winname, cv::Mat img) {
    imshow(winname, img);
    moveWindow(winname, 500, 0);
    waitKey(0);
    destroyWindow(winname);
}

Java

You can also download it from here.

 
import org.opencv.core.*;
import org.opencv.highgui.HighGui;
import org.opencv.imgcodecs.Imgcodecs;
import org.opencv.imgproc.Imgproc;
 
class Morphology_3Run {
 
    public void run(String[] args) {
 
        // Check number of arguments
        if (args.length == 0){
            System.out.println("Not enough parameters!");
            System.out.println("Program Arguments: [image_path]");
            System.exit(-1);
        }
 
        // Load the image
        Mat src = Imgcodecs.imread(args[0]);
 
        // Check if image is loaded fine
        if( src.empty() ) {
            System.out.println("Error opening image: " + args[0]);
            System.exit(-1);
        }
 
        // Show source image
        HighGui.imshow("src", src);
 
        // Transform source image to gray if it is not already
        Mat gray = new Mat();
 
        if (src.channels() == 3)
        {
            Imgproc.cvtColor(src, gray, Imgproc.COLOR_BGR2GRAY);
        }
        else
        {
            gray = src;
        }
 
        // Show gray image
        showWaitDestroy("gray" , gray);
 
        // Apply adaptiveThreshold at the bitwise_not of gray
        Mat bw = new Mat();
        Core.bitwise_not(gray, gray);
        Imgproc.adaptiveThreshold(gray, bw, 255, Imgproc.ADAPTIVE_THRESH_MEAN_C, Imgproc.THRESH_BINARY, 15, -2);
 
        // Show binary image
        showWaitDestroy("binary" , bw);
 
        // Create the images that will use to extract the horizontal and vertical lines
        Mat horizontal = bw.clone();
        Mat vertical = bw.clone();
 
        // Specify size on horizontal axis
        int horizontal_size = horizontal.cols() / 30;
 
        // Create structure element for extracting horizontal lines through morphology operations
        Mat horizontalStructure = Imgproc.getStructuringElement(Imgproc.MORPH_RECT, new Size(horizontal_size,1));
 
        // Apply morphology operations
        Imgproc.erode(horizontal, horizontal, horizontalStructure);
        Imgproc.dilate(horizontal, horizontal, horizontalStructure);
 
        // Show extracted horizontal lines
        showWaitDestroy("horizontal" , horizontal);
 
        // Specify size on vertical axis
        int vertical_size = vertical.rows() / 30;
 
        // Create structure element for extracting vertical lines through morphology operations
        Mat verticalStructure = Imgproc.getStructuringElement(Imgproc.MORPH_RECT, new Size( 1,vertical_size));
 
        // Apply morphology operations
        Imgproc.erode(vertical, vertical, verticalStructure);
        Imgproc.dilate(vertical, vertical, verticalStructure);
 
        // Show extracted vertical lines
        showWaitDestroy("vertical", vertical);
 
        // Inverse vertical image
        Core.bitwise_not(vertical, vertical);
        showWaitDestroy("vertical_bit" , vertical);
 
        // Extract edges and smooth image according to the logic
        // 1. extract edges
        // 2. dilate(edges)
        // 3. src.copyTo(smooth)
        // 4. blur smooth img
        // 5. smooth.copyTo(src, edges)
 
        // Step 1
        Mat edges = new Mat();
        Imgproc.adaptiveThreshold(vertical, edges, 255, Imgproc.ADAPTIVE_THRESH_MEAN_C, Imgproc.THRESH_BINARY, 3, -2);
        showWaitDestroy("edges", edges);
 
        // Step 2
        Mat kernel = Mat.ones(2, 2, CvType.CV_8UC1);
        Imgproc.dilate(edges, edges, kernel);
        showWaitDestroy("dilate", edges);
 
        // Step 3
        Mat smooth = new Mat();
        vertical.copyTo(smooth);
 
        // Step 4
        Imgproc.blur(smooth, smooth, new Size(2, 2));
 
        // Step 5
        smooth.copyTo(vertical, edges);
 
        // Show final result
        showWaitDestroy("smooth - final", vertical);
 
        System.exit(0);
    }
 
    private void showWaitDestroy(String winname, Mat img) {
        HighGui.imshow(winname, img);
        HighGui.moveWindow(winname, 500, 0);
        HighGui.waitKey(0);
        HighGui.destroyWindow(winname);
    }
}
 
public class Morphology_3 {
    public static void main(String[] args) {
        // Load the native library.
        System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
        new Morphology_3Run().run(args);
    }
}

Python

You can also download it from here.

"""
@file morph_lines_detection.py
@brief Use morphology transformations for extracting horizontal and vertical lines sample code
"""
import numpy as np
import sys
import cv2 as cv
 
 
def show_wait_destroy(winname, img):
    cv.imshow(winname, img)
    cv.moveWindow(winname, 500, 0)
    cv.waitKey(0)
    cv.destroyWindow(winname)
 
 
def main(argv):
    # [load_image]
    # Check number of arguments
    if len(argv) < 1:
        print ('Not enough parameters')
        print ('Usage:\nmorph_lines_detection.py < path_to_image >')
        return -1
 
    # Load the image
    src = cv.imread(argv[0], cv.IMREAD_COLOR)
 
    # Check if image is loaded fine
    if src is None:
        print ('Error opening image: ' + argv[0])
        return -1
 
    # Show source image
    cv.imshow("src", src)
    # [load_image]
 
    # [gray]
    # Transform source image to gray if it is not already
    if len(src.shape) != 2:
        gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
    else:
        gray = src
 
    # Show gray image
    show_wait_destroy("gray", gray)
    # [gray]
 
    # [bin]
    # Apply adaptiveThreshold at the bitwise_not of gray, notice the ~ symbol
    gray = cv.bitwise_not(gray)
    bw = cv.adaptiveThreshold(gray, 255, cv.ADAPTIVE_THRESH_MEAN_C, \
                                cv.THRESH_BINARY, 15, -2)
    # Show binary image
    show_wait_destroy("binary", bw)
    # [bin]
 
    # [init]
    # Create the images that will use to extract the horizontal and vertical lines
    horizontal = np.copy(bw)
    vertical = np.copy(bw)
    # [init]
 
    # [horiz]
    # Specify size on horizontal axis
    cols = horizontal.shape[1]
    horizontal_size = cols // 30
 
    # Create structure element for extracting horizontal lines through morphology operations
    horizontalStructure = cv.getStructuringElement(cv.MORPH_RECT, (horizontal_size, 1))
 
    # Apply morphology operations
    horizontal = cv.erode(horizontal, horizontalStructure)
    horizontal = cv.dilate(horizontal, horizontalStructure)
 
    # Show extracted horizontal lines
    show_wait_destroy("horizontal", horizontal)
    # [horiz]
 
    # [vert]
    # Specify size on vertical axis
    rows = vertical.shape[0]
    verticalsize = rows // 30
 
    # Create structure element for extracting vertical lines through morphology operations
    verticalStructure = cv.getStructuringElement(cv.MORPH_RECT, (1, verticalsize))
 
    # Apply morphology operations
    vertical = cv.erode(vertical, verticalStructure)
    vertical = cv.dilate(vertical, verticalStructure)
 
    # Show extracted vertical lines
    show_wait_destroy("vertical", vertical)
    # [vert]
 
    # [smooth]
    # Inverse vertical image
    vertical = cv.bitwise_not(vertical)
    show_wait_destroy("vertical_bit", vertical)
 
    '''
    Extract edges and smooth image according to the logic
    1. extract edges
    2. dilate(edges)
    3. src.copyTo(smooth)
    4. blur smooth img
    5. smooth.copyTo(src, edges)
    '''
 
    # Step 1
    edges = cv.adaptiveThreshold(vertical, 255, cv.ADAPTIVE_THRESH_MEAN_C, \
                                cv.THRESH_BINARY, 3, -2)
    show_wait_destroy("edges", edges)
 
    # Step 2
    kernel = np.ones((2, 2), np.uint8)
    edges = cv.dilate(edges, kernel)
    show_wait_destroy("dilate", edges)
 
    # Step 3
    smooth = np.copy(vertical)
 
    # Step 4
    smooth = cv.blur(smooth, (2, 2))
 
    # Step 5
    (rows, cols) = np.where(edges != 0)
    vertical[rows, cols] = smooth[rows, cols]
 
    # Show final result
    show_wait_destroy("smooth - final", vertical)
    # [smooth]
 
    return 0
 
if __name__ == "__main__":
    main(sys.argv[1:])

Explanation / Result

Get image from here .

Load Image

C++

    CommandLineParser parser(argc, argv, "{@input | notes.png | input image}");
    Mat src = imread( samples::findFile( parser.get<String>("@input") ), IMREAD_COLOR);
    if (src.empty())
    {
        cout << "Could not open or find the image!\n" << endl;
        cout << "Usage: " << argv[0] << " <Input image>" << endl;
        return -1;
    }
 
    // Show source image
    imshow("src", src);

Java

        // Check number of arguments
        if (args.length == 0){
            System.out.println("Not enough parameters!");
            System.out.println("Program Arguments: [image_path]");
            System.exit(-1);
        }
 
        // Load the image
        Mat src = Imgcodecs.imread(args[0]);
 
        // Check if image is loaded fine
        if( src.empty() ) {
            System.out.println("Error opening image: " + args[0]);
            System.exit(-1);
        }
 
        // Show source image
        HighGui.imshow("src", src);

Python

    # Check number of arguments
    if len(argv) < 1:
        print ('Not enough parameters')
        print ('Usage:\nmorph_lines_detection.py < path_to_image >')
        return -1
 
    # Load the image
    src = cv.imread(argv[0], cv.IMREAD_COLOR)
 
    # Check if image is loaded fine
    if src is None:
        print ('Error opening image: ' + argv[0])
        return -1
 
    # Show source image
    cv.imshow("src", src)

Grayscale

C++

    // Transform source image to gray if it is not already
    Mat gray;
 
    if (src.channels() == 3)
    {
        cvtColor(src, gray, COLOR_BGR2GRAY);
    }
    else
    {
        gray = src;
    }
 
    // Show gray image
    show_wait_destroy("gray", gray);

Java

        // Transform source image to gray if it is not already
        Mat gray = new Mat();
 
        if (src.channels() == 3)
        {
            Imgproc.cvtColor(src, gray, Imgproc.COLOR_BGR2GRAY);
        }
        else
        {
            gray = src;
        }
 
        // Show gray image
        showWaitDestroy("gray" , gray);

Python

    # Transform source image to gray if it is not already
    if len(src.shape) != 2:
        gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
    else:
        gray = src
 
    # Show gray image
    show_wait_destroy("gray", gray)

Grayscale to Binary image

C++

    // Apply adaptiveThreshold at the bitwise_not of gray, notice the ~ symbol
    Mat bw;
    adaptiveThreshold(~gray, bw, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 15, -2);
 
    // Show binary image
    show_wait_destroy("binary", bw);

Java

        // Apply adaptiveThreshold at the bitwise_not of gray
        Mat bw = new Mat();
        Core.bitwise_not(gray, gray);
        Imgproc.adaptiveThreshold(gray, bw, 255, Imgproc.ADAPTIVE_THRESH_MEAN_C, Imgproc.THRESH_BINARY, 15, -2);
 
        // Show binary image
        showWaitDestroy("binary" , bw);

Python

    # Apply adaptiveThreshold at the bitwise_not of gray, notice the ~ symbol
    gray = cv.bitwise_not(gray)
    bw = cv.adaptiveThreshold(gray, 255, cv.ADAPTIVE_THRESH_MEAN_C, \
                                cv.THRESH_BINARY, 15, -2)
    # Show binary image
    show_wait_destroy("binary", bw)

Output images

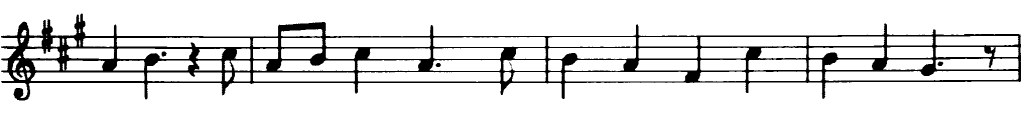
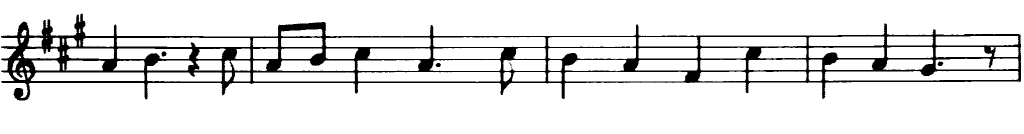
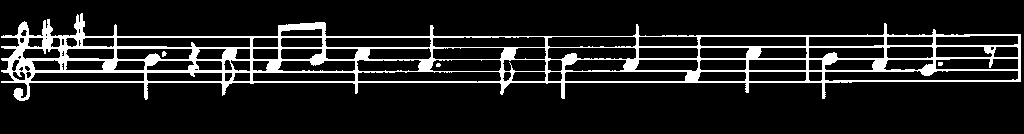
Now we are ready to apply morphological operations in order to extract the horizontal and vertical lines and as a consequence to separate the music notes from the music sheet, but first let's initialize the output images that we will use for that reason:

C++

    // Create the images that will use to extract the horizontal and vertical lines
    Mat horizontal = bw.clone();
    Mat vertical = bw.clone();

Java

        // Create the images that will use to extract the horizontal and vertical lines
        Mat horizontal = bw.clone();
        Mat vertical = bw.clone();

Python

    # Create the images that will use to extract the horizontal and vertical lines
    horizontal = np.copy(bw)
    vertical = np.copy(bw)

Structure elements

As we specified in the theory in order to extract the object that we desire, we need to create the corresponding structure element. Since we want to extract the horizontal lines, a corresponding structure element for that purpose will have the following shape:

and in the source code this is represented by the following code snippet:

C++

    // Specify size on horizontal axis
    int horizontal_size = horizontal.cols / 30;
 
    // Create structure element for extracting horizontal lines through morphology operations
    Mat horizontalStructure = getStructuringElement(MORPH_RECT, Size(horizontal_size, 1));
 
    // Apply morphology operations
    erode(horizontal, horizontal, horizontalStructure, Point(-1, -1));
    dilate(horizontal, horizontal, horizontalStructure, Point(-1, -1));
 
    // Show extracted horizontal lines
    show_wait_destroy("horizontal", horizontal);

Java

        // Specify size on horizontal axis
        int horizontal_size = horizontal.cols() / 30;
 
        // Create structure element for extracting horizontal lines through morphology operations
        Mat horizontalStructure = Imgproc.getStructuringElement(Imgproc.MORPH_RECT, new Size(horizontal_size,1));
 
        // Apply morphology operations
        Imgproc.erode(horizontal, horizontal, horizontalStructure);
        Imgproc.dilate(horizontal, horizontal, horizontalStructure);
 
        // Show extracted horizontal lines
        showWaitDestroy("horizontal" , horizontal);

Python

    # Specify size on horizontal axis
    cols = horizontal.shape[1]
    horizontal_size = cols // 30
 
    # Create structure element for extracting horizontal lines through morphology operations
    horizontalStructure = cv.getStructuringElement(cv.MORPH_RECT, (horizontal_size, 1))
 
    # Apply morphology operations
    horizontal = cv.erode(horizontal, horizontalStructure)
    horizontal = cv.dilate(horizontal, horizontalStructure)
 
    # Show extracted horizontal lines
    show_wait_destroy("horizontal", horizontal)

The same applies for the vertical lines, with the corresponding structure element: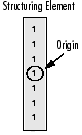

and again this is represented as follows:

C++

    // Specify size on vertical axis
    int vertical_size = vertical.rows / 30;
 
    // Create structure element for extracting vertical lines through morphology operations
    Mat verticalStructure = getStructuringElement(MORPH_RECT, Size(1, vertical_size));
 
    // Apply morphology operations
    erode(vertical, vertical, verticalStructure, Point(-1, -1));
    dilate(vertical, vertical, verticalStructure, Point(-1, -1));
 
    // Show extracted vertical lines
    show_wait_destroy("vertical", vertical);

Java

        // Specify size on vertical axis
        int vertical_size = vertical.rows() / 30;
 
        // Create structure element for extracting vertical lines through morphology operations
        Mat verticalStructure = Imgproc.getStructuringElement(Imgproc.MORPH_RECT, new Size( 1,vertical_size));
 
        // Apply morphology operations
        Imgproc.erode(vertical, vertical, verticalStructure);
        Imgproc.dilate(vertical, vertical, verticalStructure);
 
        // Show extracted vertical lines
        showWaitDestroy("vertical", vertical);

Python

    # Specify size on vertical axis
    rows = vertical.shape[0]
    verticalsize = rows // 30
 
    # Create structure element for extracting vertical lines through morphology operations
    verticalStructure = cv.getStructuringElement(cv.MORPH_RECT, (1, verticalsize))
 
    # Apply morphology operations
    vertical = cv.erode(vertical, verticalStructure)
    vertical = cv.dilate(vertical, verticalStructure)
 
    # Show extracted vertical lines
    show_wait_destroy("vertical", vertical)

Refine edges / Result

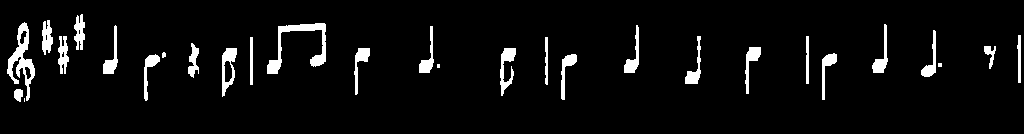
As you can see we are almost there. However, at that point you will notice that the edges of the notes are a bit rough. For that reason we need to refine the edges in order to obtain a smoother result:

C++

    // Inverse vertical image
    bitwise_not(vertical, vertical);
    show_wait_destroy("vertical_bit", vertical);
 
    // Extract edges and smooth image according to the logic
    // 1. extract edges
    // 2. dilate(edges)
    // 3. src.copyTo(smooth)
    // 4. blur smooth img
    // 5. smooth.copyTo(src, edges)
 
    // Step 1
    Mat edges;
    adaptiveThreshold(vertical, edges, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 3, -2);
    show_wait_destroy("edges", edges);
 
    // Step 2
    Mat kernel = Mat::ones(2, 2, CV_8UC1);
    dilate(edges, edges, kernel);
    show_wait_destroy("dilate", edges);
 
    // Step 3
    Mat smooth;
    vertical.copyTo(smooth);
 
    // Step 4
    blur(smooth, smooth, Size(2, 2));
 
    // Step 5
    smooth.copyTo(vertical, edges);
 
    // Show final result
    show_wait_destroy("smooth - final", vertical);

Java

        // Inverse vertical image
        Core.bitwise_not(vertical, vertical);
        showWaitDestroy("vertical_bit" , vertical);
 
        // Extract edges and smooth image according to the logic
        // 1. extract edges
        // 2. dilate(edges)
        // 3. src.copyTo(smooth)
        // 4. blur smooth img
        // 5. smooth.copyTo(src, edges)
 
        // Step 1
        Mat edges = new Mat();
        Imgproc.adaptiveThreshold(vertical, edges, 255, Imgproc.ADAPTIVE_THRESH_MEAN_C, Imgproc.THRESH_BINARY, 3, -2);
        showWaitDestroy("edges", edges);
 
        // Step 2
        Mat kernel = Mat.ones(2, 2, CvType.CV_8UC1);
        Imgproc.dilate(edges, edges, kernel);
        showWaitDestroy("dilate", edges);
 
        // Step 3
        Mat smooth = new Mat();
        vertical.copyTo(smooth);
 
        // Step 4
        Imgproc.blur(smooth, smooth, new Size(2, 2));
 
        // Step 5
        smooth.copyTo(vertical, edges);
 
        // Show final result
        showWaitDestroy("smooth - final", vertical);

Python

    # Inverse vertical image
    vertical = cv.bitwise_not(vertical)
    show_wait_destroy("vertical_bit", vertical)
 
    '''
    Extract edges and smooth image according to the logic
    1. extract edges
    2. dilate(edges)
    3. src.copyTo(smooth)
    4. blur smooth img
    5. smooth.copyTo(src, edges)
    '''
 
    # Step 1
    edges = cv.adaptiveThreshold(vertical, 255, cv.ADAPTIVE_THRESH_MEAN_C, \
                                cv.THRESH_BINARY, 3, -2)
    show_wait_destroy("edges", edges)
 
    # Step 2
    kernel = np.ones((2, 2), np.uint8)
    edges = cv.dilate(edges, kernel)
    show_wait_destroy("dilate", edges)
 
    # Step 3
    smooth = np.copy(vertical)
 
    # Step 4
    smooth = cv.blur(smooth, (2, 2))
 
    # Step 5
    (rows, cols) = np.where(edges != 0)
    vertical[rows, cols] = smooth[rows, cols]
 
    # Show final result
    show_wait_destroy("smooth - final", vertical)