 |
OpenCV 4.14.0-pre
Open Source Computer Vision
|
 |
OpenCV 4.14.0-pre
Open Source Computer Vision
|
Prev Tutorial: Extract horizontal and vertical lines by using morphological operations
Next Tutorial: Basic Thresholding Operations
| Original author | Ana Huamán |
| Compatibility | OpenCV >= 3.0 |
In this tutorial you will learn how to:
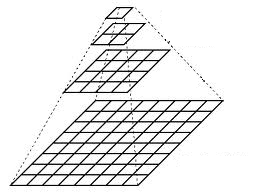
To produce layer \((i+1)\) in the Gaussian pyramid, we do the following:
\[\frac{1}{256} \begin{bmatrix} 1 & 4 & 6 & 4 & 1 \\ 4 & 16 & 24 & 16 & 4 \\ 6 & 24 & 36 & 24 & 6 \\ 4 & 16 & 24 & 16 & 4 \\ 1 & 4 & 6 & 4 & 1 \end{bmatrix}\]
This tutorial code's is shown lines below.
Let's check the general structure of the program:
Perform an infinite loop waiting for user input. Our program exits if the user presses ESC. Besides, it has two options:
Perform upsampling - Zoom 'i'n (after pressing 'i')
We use the function pyrUp() with three arguments:
Perform downsampling - Zoom 'o'ut (after pressing 'o')
We use the function pyrDown() with three arguments (similarly to pyrUp()):
Notice that it is important that the input image can be divided by a factor of two (in both dimensions). Otherwise, an error will be shown.
samples/data folder. Notice that this image is \(512 \times 512\), hence a downsample won't generate any error ( \(512 = 2^{9}\)). The original image is shown below:

