Goal

In this tutorial you will learn how to:

Use the OpenCV functions cv::ml::SVM::train to build a classifier based on SVMs and cv::ml::SVM::predict to test its performance.

What is a SVM?

A Support Vector Machine (SVM) is a discriminative classifier formally defined by a separating hyperplane. In other words, given labeled training data (supervised learning), the algorithm outputs an optimal hyperplane which categorizes new examples.

In which sense is the hyperplane obtained optimal? Let's consider the following simple problem:

For a linearly separable set of 2D-points which belong to one of two classes, find a separating straight line.

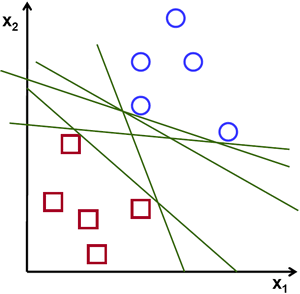
Note: In this example we deal with lines and points in the Cartesian plane instead of hyperplanes and vectors in a high dimensional space. This is a simplification of the problem.It is important to understand that this is done only because our intuition is better built from examples that are easy to imagine. However, the same concepts apply to tasks where the examples to classify lie in a space whose dimension is higher than two.

In the above picture you can see that there exists multiple lines that offer a solution to the problem. Is any of them better than the others? We can intuitively define a criterion to estimate the worth of the lines: A line is bad if it passes too close to the points because it will be noise sensitive and it will not generalize correctly. Therefore, our goal should be to find the line passing as far as possible from all points.

Then, the operation of the SVM algorithm is based on finding the hyperplane that gives the largest minimum distance to the training examples. Twice, this distance receives the important name of margin within SVM's theory. Therefore, the optimal separating hyperplane maximizes the margin of the training data.

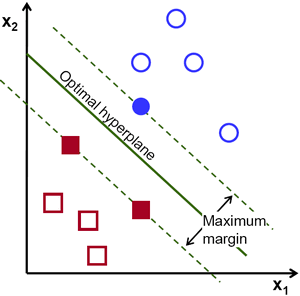
How is the optimal hyperplane computed?

Let's introduce the notation used to define formally a hyperplane:

\[f(x) = \beta_{0} + \beta^{T} x,\]

where \(\beta\) is known as the weight vector and \(\beta_{0}\) as the bias.

Note: A more in depth description of this and hyperplanes you can find in the section 4.5 (Separating Hyperplanes) of the book: Elements of Statistical Learning by T. Hastie, R. Tibshirani and J. H. Friedman ([273]).

The optimal hyperplane can be represented in an infinite number of different ways by scaling of \(\beta\) and \(\beta_{0}\). As a matter of convention, among all the possible representations of the hyperplane, the one chosen is

\[|\beta_{0} + \beta^{T} x| = 1\]

where \(x\) symbolizes the training examples closest to the hyperplane. In general, the training examples that are closest to the hyperplane are called support vectors. This representation is known as the canonical hyperplane.

Now, we use the result of geometry that gives the distance between a point \(x\) and a hyperplane \((\beta, \beta_{0})\):

\[\mathrm{distance} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||}.\]

In particular, for the canonical hyperplane, the numerator is equal to one and the distance to the support vectors is

\[\mathrm{distance}_{\text{ support vectors}} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||} = \frac{1}{||\beta||}.\]

Recall that the margin introduced in the previous section, here denoted as \(M\), is twice the distance to the closest examples:

\[M = \frac{2}{||\beta||}\]

Finally, the problem of maximizing \(M\) is equivalent to the problem of minimizing a function \(L(\beta)\) subject to some constraints. The constraints model the requirement for the hyperplane to classify correctly all the training examples \(x_{i}\). Formally,

\[\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \text{ subject to } y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \text{ } \forall i,\]

where \(y_{i}\) represents each of the labels of the training examples.

This is a problem of Lagrangian optimization that can be solved using Lagrange multipliers to obtain the weight vector \(\beta\) and the bias \(\beta_{0}\) of the optimal hyperplane.

Source Code

Explanation

Set up the training data

The training data of this exercise is formed by a set of labeled 2D-points that belong to one of two different classes; one of the classes consists of one point and the other of three points.

The function cv::ml::SVM::train that will be used afterwards requires the training data to be stored as cv::Mat objects of floats. Therefore, we create these objects from the arrays defined above:

Set up SVM's parameters

In this tutorial we have introduced the theory of SVMs in the most simple case, when the training examples are spread into two classes that are linearly separable. However, SVMs can be used in a wide variety of problems (e.g. problems with non-linearly separable data, a SVM using a kernel function to raise the dimensionality of the examples, etc). As a consequence of this, we have to define some parameters before training the SVM. These parameters are stored in an object of the class cv::ml::SVM.

Here:

Type of SVM. We choose here the type C_SVC that can be used for n-class classification (n \(\geq\) 2). The important feature of this type is that it deals with imperfect separation of classes (i.e. when the training data is non-linearly separable). This feature is not important here since the data is linearly separable and we chose this SVM type only for being the most commonly used.
Type of SVM kernel. We have not talked about kernel functions since they are not interesting for the training data we are dealing with. Nevertheless, let's explain briefly now the main idea behind a kernel function. It is a mapping done to the training data to improve its resemblance to a linearly separable set of data. This mapping consists of increasing the dimensionality of the data and is done efficiently using a kernel function. We choose here the type LINEAR which means that no mapping is done. This parameter is defined using cv::ml::SVM::setKernel.
Termination criteria of the algorithm. The SVM training procedure is implemented solving a constrained quadratic optimization problem in an iterative fashion. Here we specify a maximum number of iterations and a tolerance error so we allow the algorithm to finish in less number of steps even if the optimal hyperplane has not been computed yet. This parameter is defined in a structure cv::TermCriteria .
Train the SVM We call the method cv::ml::SVM::train to build the SVM model.

Regions classified by the SVM

The method cv::ml::SVM::predict is used to classify an input sample using a trained SVM. In this example we have used this method in order to color the space depending on the prediction done by the SVM. In other words, an image is traversed interpreting its pixels as points of the Cartesian plane. Each of the points is colored depending on the class predicted by the SVM; in green if it is the class with label 1 and in blue if it is the class with label -1.

Support vectors

We use here a couple of methods to obtain information about the support vectors. The method cv::ml::SVM::getSupportVectors obtain all of the support vectors. We have used this methods here to find the training examples that are support vectors and highlight them.

Results

The code opens an image and shows the training examples of both classes. The points of one class are represented with white circles and black ones are used for the other class.
The SVM is trained and used to classify all the pixels of the image. This results in a division of the image in a blue region and a green region. The boundary between both regions is the optimal separating hyperplane.
Finally the support vectors are shown using gray rings around the training examples.


Original author	Fernando Iglesias García
Compatibility	OpenCV >= 3.0