 |
OpenCV 4.14.0-pre
Open Source Computer Vision
|
 |
OpenCV 4.14.0-pre
Open Source Computer Vision
|
See cv::cvtColor and cv::ColorConversionCodes
Transformations within RGB space like adding/removing the alpha channel, reversing the channel order, conversion to/from 16-bit RGB color (R5:G6:B5 or R5:G5:B5), as well as conversion to/from grayscale using:
\[\text{RGB[A] to Gray:} \quad Y \leftarrow 0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot B\]
and
\[\text{Gray to RGB[A]:} \quad R \leftarrow Y, G \leftarrow Y, B \leftarrow Y, A \leftarrow \max (ChannelRange)\]
The conversion from a RGB image to gray is done with:
More advanced channel reordering can also be done with cv::mixChannels.
\[\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \leftarrow \begin{bmatrix} 0.412453 & 0.357580 & 0.180423 \\ 0.212671 & 0.715160 & 0.072169 \\ 0.019334 & 0.119193 & 0.950227 \end{bmatrix} \cdot \begin{bmatrix} R \\ G \\ B \end{bmatrix}\]
\[\begin{bmatrix} R \\ G \\ B \end{bmatrix} \leftarrow \begin{bmatrix} 3.240479 & -1.53715 & -0.498535 \\ -0.969256 & 1.875991 & 0.041556 \\ 0.055648 & -0.204043 & 1.057311 \end{bmatrix} \cdot \begin{bmatrix} X \\ Y \\ Z \end{bmatrix}\]
\(X\), \(Y\) and \(Z\) cover the whole value range (in case of floating-point images, \(Z\) may exceed 1).
\[Y \leftarrow 0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot B\]
\[Cr \leftarrow (R-Y) \cdot 0.713 + delta\]
\[Cb \leftarrow (B-Y) \cdot 0.564 + delta\]
\[R \leftarrow Y + 1.403 \cdot (Cr - delta)\]
\[G \leftarrow Y - 0.714 \cdot (Cr - delta) - 0.344 \cdot (Cb - delta)\]
\[B \leftarrow Y + 1.773 \cdot (Cb - delta)\]
where
\[delta = \left \{ \begin{array}{l l} 128 & \mbox{for 8-bit images} \\ 32768 & \mbox{for 16-bit images} \\ 0.5 & \mbox{for floating-point images} \end{array} \right .\]
Y, Cr, and Cb cover the whole value range.
Only 8-bit values are supported. The coefficients correspond to BT.601 standard with resulting values Y [16, 235], U and V [16, 240] centered at 128.
Two subsampling schemes are supported: 4:2:0 (Fourcc codes NV12, NV21, YV12, I420 and synonimic) and 4:2:2 (Fourcc codes UYVY, YUY2, YVYU and synonimic).
In both subsampling schemes Y values are written for each pixel so that Y plane is in fact a scaled and biased gray version of a source image.
In 4:2:0 scheme U and V values are averaged over 2x2 squares, i.e. only 1 U and 1 V value is saved per each 4 pixels. U and V values are saved interleaved into a separate plane (NV12, NV21) or into two separate semi-planes (YV12, I420).
In 4:2:2 scheme U and V values are averaged horizontally over each pair of pixels, i.e. only 1 U and 1 V value is saved per each 2 pixels. U and V values are saved interleaved with Y values for both pixels according to its Fourcc code.
Note that different conversions are perfomed with different precision for speed or compatibility purposes. For example, RGB to YUV 4:2:2 is converted using 14-bit fixed-point arithmetics while other conversions use 20 bits.
\[R \leftarrow 1.164 \cdot (Y - 16) + 1.596 \cdot (V - 128)\]
\[G \leftarrow 1.164 \cdot (Y - 16) - 0.813 \cdot (V - 128) - 0.391 \cdot (U - 128)\]
\[B \leftarrow 1.164 \cdot (Y - 16) + 2.018 \cdot (U - 128)\]
\[Y \leftarrow (R \cdot 0.299 + G \cdot 0.587 + B \cdot 0.114) \cdot \frac{236 - 16}{256} + 16 \]
\[U \leftarrow -0.148 \cdot R_{avg} - 0.291 \cdot G_{avg} + 0.439 \cdot B_{avg} + 128 \]
\[V \leftarrow 0.439 \cdot R_{avg} - 0.368 \cdot G_{avg} - 0.071 \cdot B_{avg} + 128 \]
In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit the 0 to 1 range.
\[V \leftarrow max(R,G,B)\]
\[S \leftarrow \fork{\frac{V-min(R,G,B)}{V}}{if \(V \neq 0\)}{0}{otherwise}\]
\[H \leftarrow \forkfour{{60(G - B)}/{(V-min(R,G,B))}}{if \(V=R\)} {{120+60(B - R)}/{(V-min(R,G,B))}}{if \(V=G\)} {{240+60(R - G)}/{(V-min(R,G,B))}}{if \(V=B\)} {0}{if \(R=G=B\)}\]
If \(H<0\) then \(H \leftarrow H+360\) . On output \(0 \leq V \leq 1\), \(0 \leq S \leq 1\), \(0 \leq H \leq 360\) .
The values are then converted to the destination data type:
In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit the 0 to 1 range.
\[V_{max} \leftarrow {max}(R,G,B)\]
\[V_{min} \leftarrow {min}(R,G,B)\]
\[L \leftarrow \frac{V_{max} + V_{min}}{2}\]
\[S \leftarrow \fork { \frac{V_{max} - V_{min}}{V_{max} + V_{min}} }{if \(L < 0.5\) } { \frac{V_{max} - V_{min}}{2 - (V_{max} + V_{min})} }{if \(L \ge 0.5\) }\]
\[H \leftarrow \forkfour {{60(G - B)}/{(V_{max}-V_{min})}}{if \(V_{max}=R\) } {{120+60(B - R)}/{(V_{max}-V_{min})}}{if \(V_{max}=G\) } {{240+60(R - G)}/{(V_{max}-V_{min})}}{if \(V_{max}=B\) } {0}{if \(R=G=B\) }\]
If \(H<0\) then \(H \leftarrow H+360\) . On output \(0 \leq L \leq 1\), \(0 \leq S \leq 1\), \(0 \leq H \leq 360\) .
The values are then converted to the destination data type:
In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit the 0 to 1 range.
\[\vecthree{X}{Y}{Z} \leftarrow \vecthreethree{0.412453}{0.357580}{0.180423}{0.212671}{0.715160}{0.072169}{0.019334}{0.119193}{0.950227} \cdot \vecthree{R}{G}{B}\]
\[X \leftarrow X/X_n, \text{where} X_n = 0.950456\]
\[Z \leftarrow Z/Z_n, \text{where} Z_n = 1.088754\]
\[L \leftarrow \fork{116*Y^{1/3}-16}{for \(Y>0.008856\)}{903.3*Y}{for \(Y \le 0.008856\)}\]
\[a \leftarrow 500 (f(X)-f(Y)) + delta\]
\[b \leftarrow 200 (f(Y)-f(Z)) + delta\]
where
\[f(t)= \fork{t^{1/3}}{for \(t>0.008856\)}{7.787 t+16/116}{for \(t\leq 0.008856\)}\]
and
\[delta = \fork{128}{for 8-bit images}{0}{for floating-point images}\]
This outputs \(0 \leq L \leq 100\), \(-127 \leq a \leq 127\), \(-127 \leq b \leq 127\) . The values are then converted to the destination data type:
In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit 0 to 1 range.
\[\vecthree{X}{Y}{Z} \leftarrow \vecthreethree{0.412453}{0.357580}{0.180423}{0.212671}{0.715160}{0.072169}{0.019334}{0.119193}{0.950227} \cdot \vecthree{R}{G}{B}\]
\[L \leftarrow \fork{116*Y^{1/3} - 16}{for \(Y>0.008856\)}{903.3 Y}{for \(Y\leq 0.008856\)}\]
\[u' \leftarrow 4*X/(X + 15*Y + 3 Z)\]
\[v' \leftarrow 9*Y/(X + 15*Y + 3 Z)\]
\[u \leftarrow 13*L*(u' - u_n) \quad \text{where} \quad u_n=0.19793943\]
\[v \leftarrow 13*L*(v' - v_n) \quad \text{where} \quad v_n=0.46831096\]
This outputs \(0 \leq L \leq 100\), \(-134 \leq u \leq 220\), \(-140 \leq v \leq 122\) .
The values are then converted to the destination data type:
Note that when converting integer Luv images to RGB the intermediate X, Y and Z values are truncated to \( [0, 2] \) range to fit white point limitations. It may lead to incorrect representation of colors with odd XYZ values.
The above formulae for converting RGB to/from various color spaces have been taken from multiple sources on the web, primarily from the Charles Poynton site http://www.poynton.com/ColorFAQ.html
The Bayer pattern is widely used in CCD and CMOS cameras. It enables you to get color pictures from a single plane where R, G, and B pixels (sensors of a particular component) are interleaved as follows:
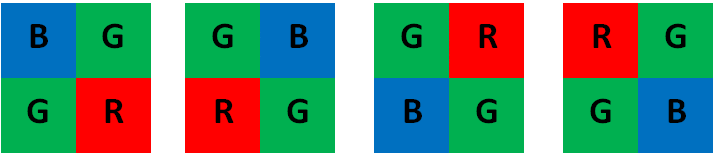
The output RGB components of a pixel are interpolated from 1, 2, or 4 neighbors of the pixel having the same color.

There are several modifications of the above pattern that can be achieved by shifting the pattern one pixel left and/or one pixel up. The two letters \(C_1\) and \(C_2\) in the conversion constants CV_Bayer \(C_1 C_2\) 2BGR and CV_Bayer \(C_1 C_2\) 2RGB indicate the particular pattern type. These are components from the second row, second and third columns, respectively. For example, the above pattern has a very popular "BG" type.