 |
OpenCV
4.9.0-dev
Open Source Computer Vision
|
 |
OpenCV
4.9.0-dev
Open Source Computer Vision
|
The pose computation problem [181] consists in solving for the rotation and translation that minimizes the reprojection error from 3D-2D point correspondences.
The solvePnP and related functions estimate the object pose given a set of object points, their corresponding image projections, as well as the camera intrinsic matrix and the distortion coefficients, see the figure below (more precisely, the X-axis of the camera frame is pointing to the right, the Y-axis downward and the Z-axis forward).
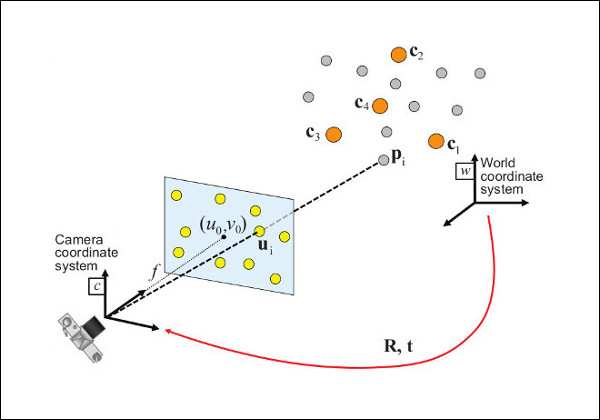
Points expressed in the world frame \( \bf{X}_w \) are projected into the image plane \( \left[ u, v \right] \) using the perspective projection model \( \Pi \) and the camera intrinsic parameters matrix \( \bf{A} \) (also denoted \( \bf{K} \) in the literature):
\[ \begin{align*} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \bf{A} \hspace{0.1em} \Pi \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]
The estimated pose is thus the rotation (rvec) and the translation (tvec) vectors that allow transforming a 3D point expressed in the world frame into the camera frame:
\[ \begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]
Refer to the cv::SolvePnPMethod enum documentation for the list of possible values. Some details about each method are described below:
The cv::solveP3P() computes an object pose from exactly 3 3D-2D point correspondences. A P3P problem has up to 4 solutions.
The cv::solvePnP() returns the rotation and the translation vectors that transform a 3D point expressed in the object coordinate frame to the camera coordinate frame, using different methods:
The cv::solvePnPGeneric() allows retrieving all the possible solutions.
Currently, only cv::SOLVEPNP_P3P, cv::SOLVEPNP_AP3P, cv::SOLVEPNP_IPPE, cv::SOLVEPNP_IPPE_SQUARE, cv::SOLVEPNP_SQPNP can return multiple solutions.
The cv::solvePnPRansac() computes the object pose wrt. the camera frame using a RANSAC scheme to deal with outliers.
More information can be found in [324]
Pose refinement consists in estimating the rotation and translation that minimizes the reprojection error using a non-linear minimization method and starting from an initial estimate of the solution. OpenCV proposes cv::solvePnPRefineLM() and cv::solvePnPRefineVVS() for this problem.
cv::solvePnPRefineLM() uses a non-linear Levenberg-Marquardt minimization scheme [177] [77] and the current implementation computes the rotation update as a perturbation and not on SO(3).
cv::solvePnPRefineVVS() uses a Gauss-Newton non-linear minimization scheme [181] and with an update of the rotation part computed using the exponential map.
 1.9.8
1.9.8