Perspective-n-Point (PnP) pose computation

Pose computation overview

The pose computation problem [186] consists in solving for the rotation and translation that minimizes the reprojection error from 3D-2D point correspondences.

The solvePnP and related functions estimate the object pose given a set of object points, their corresponding image projections, as well as the camera intrinsic matrix and the distortion coefficients, see the figure below (more precisely, the convention in the computer vision field is to have the X-axis of the camera frame pointing to the right, the Y-axis downward and the Z-axis forward).

Top: the 6 dof pose computed from a list of 3D-2D point correspondences. Bottom: the considered perspective projection model.

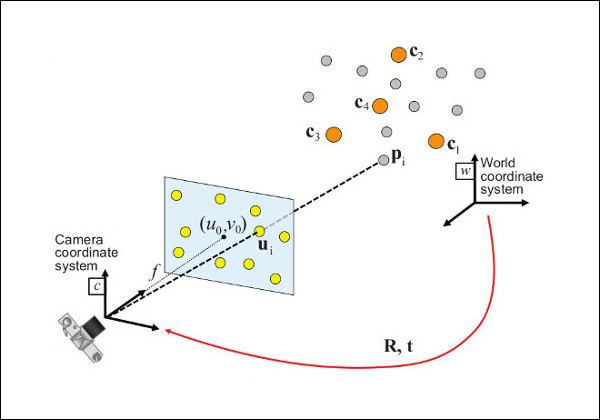
Points expressed in the world frame \( \bf{X}_w \) are projected into the image plane \( \left[ u, v \right] \) using the perspective projection model \( \Pi \) and the camera intrinsic parameters matrix \( \bf{A} \) (also denoted \( \bf{K} \) in the literature):

\[ \begin{align*} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \bf{A} \hspace{0.1em} \Pi \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]

The estimated pose is thus the rotation (rvec) and the translation (tvec) vectors that allow transforming a 3D point expressed in the world frame into the camera frame:

\[ \begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]

Pose computation methods

Refer to the cv::SolvePnPMethod enum documentation for the list of possible values. Some details about each method are described below:

• cv::SOLVEPNP_ITERATIVE Iterative method is based on a Levenberg-Marquardt optimization. In this case the function finds such a pose that minimizes reprojection error, that is the sum of squared distances between the observed projections "imagePoints" and the projected (using cv::projectPoints ) "objectPoints". Initial solution for non-planar "objectPoints" needs at least 6 points and uses the DLT algorithm. Initial solution for planar "objectPoints" needs at least 4 points and uses pose from homography decomposition.
• cv::SOLVEPNP_P3P Method is based on the paper of Ding, Y., Yang, J., Larsson, V., Olsson, C., & Åstrom, K. "Revisiting the P3P Problem" ([73]). In this case the function requires exactly four object and image points.
• cv::SOLVEPNP_AP3P Method is based on the paper of T. Ke, S. Roumeliotis "An Efficient Algebraic Solution to the Perspective-Three-Point Problem" ([148]). In this case the function requires exactly four object and image points.
• cv::SOLVEPNP_EPNP Method has been introduced by F. Moreno-Noguer, V. Lepetit and P. Fua in the paper "EPnP: Efficient Perspective-n-Point Camera Pose Estimation" ([161]).
• cv::SOLVEPNP_DLS Broken implementation. Using this flag will fallback to EPnP.
  Method is based on the paper of J. Hesch and S. Roumeliotis. "A Direct Least-Squares (DLS) Method for PnP" ([128]).
• cv::SOLVEPNP_UPNP Broken implementation. Using this flag will fallback to EPnP.
  Method is based on the paper of A. Penate-Sanchez, J. Andrade-Cetto, F. Moreno-Noguer. "Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation" ([218]). In this case the function also estimates the parameters \(f_x\) and \(f_y\) assuming that both have the same value. Then the cameraMatrix is updated with the estimated focal length.
• cv::SOLVEPNP_IPPE Method is based on the paper of T. Collins and A. Bartoli. "Infinitesimal Plane-Based Pose Estimation" ([64]). This method requires coplanar object points.
• cv::SOLVEPNP_IPPE_SQUARE Method is based on the paper of Toby Collins and Adrien Bartoli. "Infinitesimal Plane-Based Pose Estimation" ([64]). This method is suitable for marker pose estimation. It requires 4 coplanar object points defined in the following order:
  • point 0: [-squareLength / 2, squareLength / 2, 0]
  • point 1: [ squareLength / 2, squareLength / 2, 0]
  • point 2: [ squareLength / 2, -squareLength / 2, 0]
  • point 3: [-squareLength / 2, -squareLength / 2, 0]
• cv::SOLVEPNP_SQPNP Method is based on the paper "A Consistently Fast and Globally Optimal Solution to the Perspective-n-Point Problem" by G. Terzakis and M.Lourakis ([272]). It requires 3 or more points.

P3P

The cv::solveP3P() computes an object pose from exactly 3 3D-2D point correspondences. A P3P problem has up to 4 solutions.

Note

The solutions are sorted by reprojection errors (lowest to highest).

PnP

The cv::solvePnP() returns the rotation and the translation vectors that transform a 3D point expressed in the object coordinate frame to the camera coordinate frame, using different methods:

• P3P methods (cv::SOLVEPNP_P3P, cv::SOLVEPNP_AP3P): need 4 input points to return a unique solution.
• cv::SOLVEPNP_IPPE Input points must be >= 4 and object points must be coplanar.
• cv::SOLVEPNP_IPPE_SQUARE Special case suitable for marker pose estimation. Number of input points must be 4. Object points must be defined in the following order:
  • point 0: [-squareLength / 2, squareLength / 2, 0]
  • point 1: [ squareLength / 2, squareLength / 2, 0]
  • point 2: [ squareLength / 2, -squareLength / 2, 0]
  • point 3: [-squareLength / 2, -squareLength / 2, 0]
• for all the other flags, number of input points must be >= 4 and object points can be in any configuration.

Generic PnP

The cv::solvePnPGeneric() allows retrieving all the possible solutions.

Currently, only cv::SOLVEPNP_P3P, cv::SOLVEPNP_AP3P, cv::SOLVEPNP_IPPE, cv::SOLVEPNP_IPPE_SQUARE, cv::SOLVEPNP_SQPNP can return multiple solutions.

RANSAC PnP

The cv::solvePnPRansac() computes the object pose wrt. the camera frame using a RANSAC scheme to deal with outliers.

More information can be found in [329]

Pose refinement

Pose refinement consists in estimating the rotation and translation that minimizes the reprojection error using a non-linear minimization method and starting from an initial estimate of the solution. OpenCV proposes cv::solvePnPRefineLM() and cv::solvePnPRefineVVS() for this problem.

cv::solvePnPRefineLM() uses a non-linear Levenberg-Marquardt minimization scheme [182] [81] and the current implementation computes the rotation update as a perturbation and not on SO(3).

cv::solvePnPRefineVVS() uses a Gauss-Newton non-linear minimization scheme [186] and with an update of the rotation part computed using the exponential map.

Note

at least three 3D-2D point correspondences are necessary.