 |
OpenCV 4.14.0-pre
Open Source Computer Vision
|
 |
OpenCV 4.14.0-pre
Open Source Computer Vision
|
Prev Tutorial: Affine Transformations
Next Tutorial: Histogram Calculation
| Original author | Ana Huamán |
| Compatibility | OpenCV >= 3.0 |
In this tutorial you will learn:
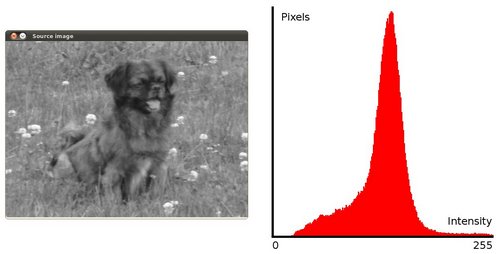
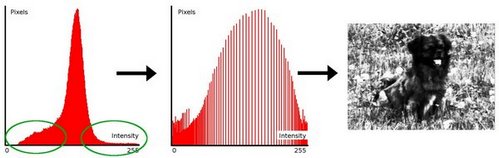
To accomplish the equalization effect, the remapping should be the cumulative distribution function (cdf) (more details, refer to Learning OpenCV). For the histogram \(H(i)\), its cumulative distribution \(H^{'}(i)\) is:
\[H^{'}(i) = \sum_{0 \le j < i} H(j)\]
To use this as a remapping function, we have to normalize \(H^{'}(i)\) such that the maximum value is 255 ( or the maximum value for the intensity of the image ). From the example above, the cumulative function is:
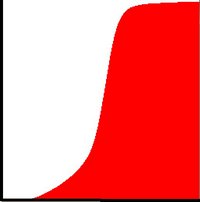
Finally, we use a simple remapping procedure to obtain the intensity values of the equalized image:
\[equalized( x, y ) = H^{'}( src(x,y) )\]
Load the source image:
Convert it to grayscale:
Apply histogram equalization with the function cv::equalizeHist :
As it can be easily seen, the only arguments are the original image and the output (equalized) image.
Display both images (original and equalized):
Wait until user exists the program

which, by the way, has this histogram:
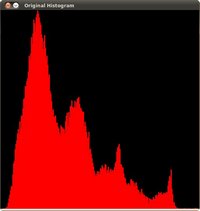
notice that the pixels are clustered around the center of the histogram.

this image has certainly more contrast. Check out its new histogram like this:
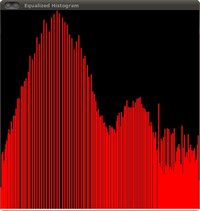
Notice how the number of pixels is more distributed through the intensity range.