 |
OpenCV
Open Source Computer Vision
|
 |
OpenCV
Open Source Computer Vision
|
Prev Tutorial: Random generator and text with OpenCV
Next Tutorial: Eroding and Dilating
In this tutorial you will learn how to apply diverse linear filters to smooth images using OpenCV functions such as:
To perform a smoothing operation we will apply a filter to our image. The most common type of filters are linear, in which an output pixel's value (i.e. g(i,j)) is determined as a weighted sum of input pixel values (i.e. f(i+k,j+l)) :
g(i,j) = \sum_{k,l} f(i+k, j+l) h(k,l)
h(k,l) is called the kernel, which is nothing more than the coefficients of the filter.
It helps to visualize a filter as a window of coefficients sliding across the image.
The kernel is below:
K = \dfrac{1}{K_{width} \cdot K_{height}} \begin{bmatrix} 1 & 1 & 1 & ... & 1 \\ 1 & 1 & 1 & ... & 1 \\ . & . & . & ... & 1 \\ . & . & . & ... & 1 \\ 1 & 1 & 1 & ... & 1 \end{bmatrix}
Just to make the picture clearer, remember how a 1D Gaussian kernel look like?
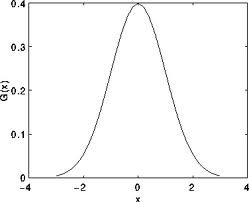
Assuming that an image is 1D, you can notice that the pixel located in the middle would have the biggest weight. The weight of its neighbors decreases as the spatial distance between them and the center pixel increases.
G_{0}(x, y) = A e^{ \dfrac{ -(x - \mu_{x})^{2} }{ 2\sigma^{2}_{x} } + \dfrac{ -(y - \mu_{y})^{2} }{ 2\sigma^{2}_{y} } }
where \mu is the mean (the peak) and \sigma^{2} represents the variance (per each of the variables x and y)The median filter run through each element of the signal (in this case the image) and replace each pixel with the median of its neighboring pixels (located in a square neighborhood around the evaluated pixel).
Let's check the OpenCV functions that involve only the smoothing procedure, since the rest is already known by now.
Here is a snapshot of the image smoothed using medianBlur:

 1.8.13
1.8.13