In this tutorial you will learn how to:
Note
The explanation below belongs to the book Computer Vision: Algorithms and Applications by Richard Szeliski
Two commonly used point processes are multiplication and addition with a constant:
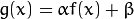
The parameters  and
and  are often called the gain and bias parameters; sometimes these parameters are said to control contrast and brightness respectively.
are often called the gain and bias parameters; sometimes these parameters are said to control contrast and brightness respectively.
You can think of 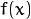 as the source image pixels and
as the source image pixels and  as the output image pixels. Then, more conveniently we can write the expression as:
as the output image pixels. Then, more conveniently we can write the expression as:
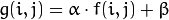
where  and
and  indicates that the pixel is located in the i-th row and j-th column.
indicates that the pixel is located in the i-th row and j-th column.
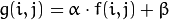 :
:#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
double alpha; /*< Simple contrast control */
int beta; /*< Simple brightness control */
int main( int argc, char** argv )
{
/// Read image given by user
Mat image = imread( argv[1] );
Mat new_image = Mat::zeros( image.size(), image.type() );
/// Initialize values
std::cout<<" Basic Linear Transforms "<<std::endl;
std::cout<<"-------------------------"<<std::endl;
std::cout<<"* Enter the alpha value [1.0-3.0]: ";std::cin>>alpha;
std::cout<<"* Enter the beta value [0-100]: "; std::cin>>beta;
/// Do the operation new_image(i,j) = alpha*image(i,j) + beta
for( int y = 0; y < image.rows; y++ ) {
for( int x = 0; x < image.cols; x++ ) {
for( int c = 0; c < 3; c++ ) {
new_image.at<Vec3b>(y,x)[c] =
saturate_cast<uchar>( alpha*( image.at<Vec3b>(y,x)[c] ) + beta );
}
}
}
/// Create Windows
namedWindow("Original Image", 1);
namedWindow("New Image", 1);
/// Show stuff
imshow("Original Image", image);
imshow("New Image", new_image);
/// Wait until user press some key
waitKey();
return 0;
}
We begin by creating parameters to save  and
and  to be entered by the user:
to be entered by the user:
double alpha;
int beta;
We load an image using imread and save it in a Mat object:
Mat image = imread( argv[1] );
Now, since we will make some transformations to this image, we need a new Mat object to store it. Also, we want this to have the following features:
Mat new_image = Mat::zeros( image.size(), image.type() );
We observe that Mat::zeros returns a Matlab-style zero initializer based on image.size() and image.type()
Now, to perform the operation 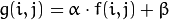 we will access to each pixel in image. Since we are operating with RGB images, we will have three values per pixel (R, G and B), so we will also access them separately. Here is the piece of code:
we will access to each pixel in image. Since we are operating with RGB images, we will have three values per pixel (R, G and B), so we will also access them separately. Here is the piece of code:
for( int y = 0; y < image.rows; y++ ) {
for( int x = 0; x < image.cols; x++ ) {
for( int c = 0; c < 3; c++ ) {
new_image.at<Vec3b>(y,x)[c] =
saturate_cast<uchar>( alpha*( image.at<Vec3b>(y,x)[c] ) + beta );
}
}
}
Notice the following:
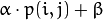 can give values out of range or not integers (if
can give values out of range or not integers (if  is float), we use saturate_cast to make sure the values are valid.
is float), we use saturate_cast to make sure the values are valid.Finally, we create windows and show the images, the usual way.
namedWindow("Original Image", 1);
namedWindow("New Image", 1);
imshow("Original Image", image);
imshow("New Image", new_image);
waitKey(0);
Note
Instead of using the for loops to access each pixel, we could have simply used this command:
image.convertTo(new_image, -1, alpha, beta);
where convertTo would effectively perform new_image = a*image + beta. However, we wanted to show you how to access each pixel. In any case, both methods give the same result but convertTo is more optimized and works a lot faster.
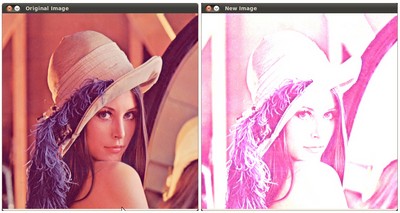
Running our code and using 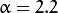 and
and 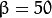
$ ./BasicLinearTransforms lena.jpg
Basic Linear Transforms
-------------------------
* Enter the alpha value [1.0-3.0]: 2.2
* Enter the beta value [0-100]: 50
We get this: