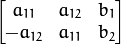Motion Analysis and Object Tracking¶
calcOpticalFlowPyrLK¶
Calculates an optical flow for a sparse feature set using the iterative Lucas-Kanade method with pyramids.
-
C++:
calcOpticalFlowPyrLK(InputArray prevImg, InputArray nextImg, InputArray prevPts, InputOutputArray nextPts, OutputArray status, OutputArray err, Size winSize=Size(21,21), int maxLevel=3, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01), int flags=0, double minEigThreshold=1e-4 )¶
-
Python:
cv2.calcOpticalFlowPyrLK(prevImg, nextImg, prevPts[, nextPts[, status[, err[, winSize[, maxLevel[, criteria[, flags[, minEigThreshold]]]]]]]]) → nextPts, status, err¶
-
C:
cvCalcOpticalFlowPyrLK(const CvArr* prev, const CvArr* curr, CvArr* prev_pyr, CvArr* curr_pyr, const CvPoint2D32f* prev_features, CvPoint2D32f* curr_features, int count, CvSize win_size, int level, char* status, float* track_error, CvTermCriteria criteria, int flags)¶
-
Python:
cv.CalcOpticalFlowPyrLK(prev, curr, prevPyr, currPyr, prevFeatures, winSize, level, criteria, flags, guesses=None) -> (currFeatures, status, track_error)¶ Parameters: - prevImg – first 8-bit input image or pyramid constructed by
buildOpticalFlowPyramid(). - nextImg – second input image or pyramid of the same size and the same type as
prevImg. - prevPts – vector of 2D points for which the flow needs to be found; point coordinates must be single-precision floating-point numbers.
- nextPts – output vector of 2D points (with single-precision floating-point coordinates) containing the calculated new positions of input features in the second image; when
OPTFLOW_USE_INITIAL_FLOWflag is passed, the vector must have the same size as in the input. - status – output status vector (of unsigned chars); each element of the vector is set to 1 if the flow for the corresponding features has been found, otherwise, it is set to 0.
- err – output vector of errors; each element of the vector is set to an error for the corresponding feature, type of the error measure can be set in
flagsparameter; if the flow wasn’t found then the error is not defined (use thestatusparameter to find such cases). - winSize – size of the search window at each pyramid level.
- maxLevel – 0-based maximal pyramid level number; if set to 0, pyramids are not used (single level), if set to 1, two levels are used, and so on; if pyramids are passed to input then algorithm will use as many levels as pyramids have but no more than
maxLevel. - criteria – parameter, specifying the termination criteria of the iterative search algorithm (after the specified maximum number of iterations
criteria.maxCountor when the search window moves by less thancriteria.epsilon. - flags –
operation flags:
- OPTFLOW_USE_INITIAL_FLOW uses initial estimations, stored in
nextPts; if the flag is not set, thenprevPtsis copied tonextPtsand is considered the initial estimate. - OPTFLOW_LK_GET_MIN_EIGENVALS use minimum eigen values as an error measure (see
minEigThresholddescription); if the flag is not set, then L1 distance between patches around the original and a moved point, divided by number of pixels in a window, is used as a error measure.
- OPTFLOW_USE_INITIAL_FLOW uses initial estimations, stored in
- minEigThreshold – the algorithm calculates the minimum eigen value of a 2x2 normal matrix of optical flow equations (this matrix is called a spatial gradient matrix in [Bouguet00]), divided by number of pixels in a window; if this value is less than
minEigThreshold, then a corresponding feature is filtered out and its flow is not processed, so it allows to remove bad points and get a performance boost.
- prevImg – first 8-bit input image or pyramid constructed by
The function implements a sparse iterative version of the Lucas-Kanade optical flow in pyramids. See [Bouguet00]. The function is parallelized with the TBB library.
Note
- An example using the Lucas-Kanade optical flow algorithm can be found at opencv_source_code/samples/cpp/lkdemo.cpp
- (Python) An example using the Lucas-Kanade optical flow algorithm can be found at opencv_source_code/samples/python2/lk_track.py
- (Python) An example using the Lucas-Kanade tracker for homography matching can be found at opencv_source_code/samples/python2/lk_homography.py
buildOpticalFlowPyramid¶
Constructs the image pyramid which can be passed to calcOpticalFlowPyrLK().
-
C++:
buildOpticalFlowPyramid(InputArray img, OutputArrayOfArrays pyramid, Size winSize, int maxLevel, bool withDerivatives=true, int pyrBorder=BORDER_REFLECT_101, int derivBorder=BORDER_CONSTANT, bool tryReuseInputImage=true)¶
-
Python:
cv2.buildOpticalFlowPyramid(img, winSize, maxLevel[, pyramid[, withDerivatives[, pyrBorder[, derivBorder[, tryReuseInputImage]]]]]) → retval, pyramid¶ Parameters: - img – 8-bit input image.
- pyramid – output pyramid.
- winSize – window size of optical flow algorithm. Must be not less than
winSizeargument ofcalcOpticalFlowPyrLK(). It is needed to calculate required padding for pyramid levels. - maxLevel – 0-based maximal pyramid level number.
- withDerivatives – set to precompute gradients for the every pyramid level. If pyramid is constructed without the gradients then
calcOpticalFlowPyrLK()will calculate them internally. - pyrBorder – the border mode for pyramid layers.
- derivBorder – the border mode for gradients.
- tryReuseInputImage – put ROI of input image into the pyramid if possible. You can pass
falseto force data copying.
Returns: number of levels in constructed pyramid. Can be less than
maxLevel.
calcOpticalFlowFarneback¶
Computes a dense optical flow using the Gunnar Farneback’s algorithm.
-
C++:
calcOpticalFlowFarneback(InputArray prev, InputArray next, InputOutputArray flow, double pyr_scale, int levels, int winsize, int iterations, int poly_n, double poly_sigma, int flags)¶
-
C:
cvCalcOpticalFlowFarneback(const CvArr* prev, const CvArr* next, CvArr* flow, double pyr_scale, int levels, int winsize, int iterations, int poly_n, double poly_sigma, int flags)¶
-
Python:
cv2.calcOpticalFlowFarneback(prev, next, pyr_scale, levels, winsize, iterations, poly_n, poly_sigma, flags[, flow]) → flow¶ Parameters: - prev – first 8-bit single-channel input image.
- next – second input image of the same size and the same type as
prev. - flow – computed flow image that has the same size as
prevand typeCV_32FC2. - pyr_scale – parameter, specifying the image scale (<1) to build pyramids for each image;
pyr_scale=0.5means a classical pyramid, where each next layer is twice smaller than the previous one. - levels – number of pyramid layers including the initial image;
levels=1means that no extra layers are created and only the original images are used. - winsize – averaging window size; larger values increase the algorithm robustness to image noise and give more chances for fast motion detection, but yield more blurred motion field.
- iterations – number of iterations the algorithm does at each pyramid level.
- poly_n – size of the pixel neighborhood used to find polynomial expansion in each pixel; larger values mean that the image will be approximated with smoother surfaces, yielding more robust algorithm and more blurred motion field, typically
poly_n=5 or 7. - poly_sigma – standard deviation of the Gaussian that is used to smooth derivatives used as a basis for the polynomial expansion; for
poly_n=5, you can setpoly_sigma=1.1, forpoly_n=7, a good value would bepoly_sigma=1.5. - flags –
operation flags that can be a combination of the following:
- OPTFLOW_USE_INITIAL_FLOW uses the input
flowas an initial flow approximation. - OPTFLOW_FARNEBACK_GAUSSIAN uses the Gaussian
 filter instead of a box filter of the same size for optical flow estimation; usually, this option gives z more accurate flow than with a box filter, at the cost of lower speed; normally,
filter instead of a box filter of the same size for optical flow estimation; usually, this option gives z more accurate flow than with a box filter, at the cost of lower speed; normally, winsizefor a Gaussian window should be set to a larger value to achieve the same level of robustness.
- OPTFLOW_USE_INITIAL_FLOW uses the input
The function finds an optical flow for each prev pixel using the [Farneback2003] algorithm so that
![\texttt{prev} (y,x) \sim \texttt{next} ( y + \texttt{flow} (y,x)[1], x + \texttt{flow} (y,x)[0])](../../../_images/math/fbf93c97d884d92c45f13996a3698283840829cd.png)
Note
- An example using the optical flow algorithm described by Gunnar Farneback can be found at opencv_source_code/samples/cpp/fback.cpp
- (Python) An example using the optical flow algorithm described by Gunnar Farneback can be found at opencv_source_code/samples/python2/opt_flow.py
estimateRigidTransform¶
Computes an optimal affine transformation between two 2D point sets.
-
C++:
estimateRigidTransform(InputArray src, InputArray dst, bool fullAffine)¶
-
Python:
cv2.estimateRigidTransform(src, dst, fullAffine) → retval¶ Parameters: - src – First input 2D point set stored in
std::vectororMat, or an image stored inMat. - dst – Second input 2D point set of the same size and the same type as
A, or another image. - fullAffine – If true, the function finds an optimal affine transformation with no additional restrictions (6 degrees of freedom). Otherwise, the class of transformations to choose from is limited to combinations of translation, rotation, and uniform scaling (5 degrees of freedom).
- src – First input 2D point set stored in
The function finds an optimal affine transform [A|b] (a 2 x 3 floating-point matrix) that approximates best the affine transformation between:
- Two point sets
- Two raster images. In this case, the function first finds some features in the
srcimage and finds the corresponding features indstimage. After that, the problem is reduced to the first case.
In case of point sets, the problem is formulated as follows: you need to find a 2x2 matrix A and 2x1 vector b so that:
where
src[i]anddst[i]are the i-th points insrcanddst, respectively
can be either arbitrary (when
fullAffine=true) or have a form of
when
fullAffine=false.
updateMotionHistory¶
Updates the motion history image by a moving silhouette.
-
C++:
updateMotionHistory(InputArray silhouette, InputOutputArray mhi, double timestamp, double duration)¶
-
Python:
cv2.updateMotionHistory(silhouette, mhi, timestamp, duration) → None¶
-
C:
cvUpdateMotionHistory(const CvArr* silhouette, CvArr* mhi, double timestamp, double duration)¶
-
Python:
cv.UpdateMotionHistory(silhouette, mhi, timestamp, duration) → None¶ Parameters: - silhouette – Silhouette mask that has non-zero pixels where the motion occurs.
- mhi – Motion history image that is updated by the function (single-channel, 32-bit floating-point).
- timestamp – Current time in milliseconds or other units.
- duration – Maximal duration of the motion track in the same units as
timestamp.
The function updates the motion history image as follows:
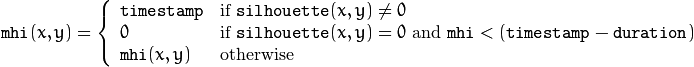
That is, MHI pixels where the motion occurs are set to the current timestamp , while the pixels where the motion happened last time a long time ago are cleared.
The function, together with
calcMotionGradient() and
calcGlobalOrientation() , implements a motion templates technique described in
[Davis97] and [Bradski00].
See also the OpenCV sample motempl.c that demonstrates the use of all the motion template functions.
calcMotionGradient¶
Calculates a gradient orientation of a motion history image.
-
C++:
calcMotionGradient(InputArray mhi, OutputArray mask, OutputArray orientation, double delta1, double delta2, int apertureSize=3 )¶
-
Python:
cv2.calcMotionGradient(mhi, delta1, delta2[, mask[, orientation[, apertureSize]]]) → mask, orientation¶
-
C:
cvCalcMotionGradient(const CvArr* mhi, CvArr* mask, CvArr* orientation, double delta1, double delta2, int aperture_size=3 )¶
-
Python:
cv.CalcMotionGradient(mhi, mask, orientation, delta1, delta2, apertureSize=3) → None¶ Parameters: - mhi – Motion history single-channel floating-point image.
- mask – Output mask image that has the type
CV_8UC1and the same size asmhi. Its non-zero elements mark pixels where the motion gradient data is correct. - orientation – Output motion gradient orientation image that has the same type and the same size as
mhi. Each pixel of the image is a motion orientation, from 0 to 360 degrees. - delta1 – Minimal (or maximal) allowed difference between
mhivalues within a pixel neighborhood. - delta2 –
Maximal (or minimal) allowed difference between
mhivalues within a pixel neighborhood. That is, the function finds the minimum (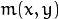 ) and maximum (
) and maximum ( 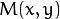 )
) mhivalues over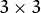 neighborhood of each pixel and marks the motion orientation at
neighborhood of each pixel and marks the motion orientation at 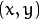 as valid only if
as valid only if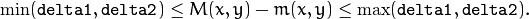
- apertureSize – Aperture size of the
Sobel()operator.
The function calculates a gradient orientation at each pixel
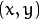 as:
as:
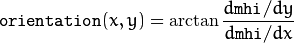
In fact,
fastAtan2() and
phase() are used so that the computed angle is measured in degrees and covers the full range 0..360. Also, the mask is filled to indicate pixels where the computed angle is valid.
Note
- (Python) An example on how to perform a motion template technique can be found at opencv_source_code/samples/python2/motempl.py
calcGlobalOrientation¶
Calculates a global motion orientation in a selected region.
-
C++:
calcGlobalOrientation(InputArray orientation, InputArray mask, InputArray mhi, double timestamp, double duration)¶
-
Python:
cv2.calcGlobalOrientation(orientation, mask, mhi, timestamp, duration) → retval¶
-
C:
cvCalcGlobalOrientation(const CvArr* orientation, const CvArr* mask, const CvArr* mhi, double timestamp, double duration)¶
-
Python:
cv.CalcGlobalOrientation(orientation, mask, mhi, timestamp, duration) → float¶ Parameters: - orientation – Motion gradient orientation image calculated by the function
calcMotionGradient(). - mask – Mask image. It may be a conjunction of a valid gradient mask, also calculated by
calcMotionGradient(), and the mask of a region whose direction needs to be calculated. - mhi – Motion history image calculated by
updateMotionHistory(). - timestamp – Timestamp passed to
updateMotionHistory(). - duration – Maximum duration of a motion track in milliseconds, passed to
updateMotionHistory().
- orientation – Motion gradient orientation image calculated by the function
The function calculates an average
motion direction in the selected region and returns the angle between
0 degrees and 360 degrees. The average direction is computed from
the weighted orientation histogram, where a recent motion has a larger
weight and the motion occurred in the past has a smaller weight, as recorded in mhi .
segmentMotion¶
Splits a motion history image into a few parts corresponding to separate independent motions (for example, left hand, right hand).
-
C++:
segmentMotion(InputArray mhi, OutputArray segmask, vector<Rect>& boundingRects, double timestamp, double segThresh)¶
-
Python:
cv2.segmentMotion(mhi, timestamp, segThresh[, segmask]) → segmask, boundingRects¶
-
C:
cvSegmentMotion(const CvArr* mhi, CvArr* seg_mask, CvMemStorage* storage, double timestamp, double seg_thresh)¶
-
Python:
cv.SegmentMotion(mhi, seg_mask, storage, timestamp, seg_thresh) → boundingRects¶ Parameters: - mhi – Motion history image.
- segmask – Image where the found mask should be stored, single-channel, 32-bit floating-point.
- boundingRects – Vector containing ROIs of motion connected components.
- timestamp – Current time in milliseconds or other units.
- segThresh – Segmentation threshold that is recommended to be equal to the interval between motion history “steps” or greater.
The function finds all of the motion segments and marks them in segmask with individual values (1,2,...). It also computes a vector with ROIs of motion connected components. After that the motion direction for every component can be calculated with calcGlobalOrientation() using the extracted mask of the particular component.
CamShift¶
Finds an object center, size, and orientation.
-
C++:
CamShift(InputArray probImage, Rect& window, TermCriteria criteria)¶
-
Python:
cv2.CamShift(probImage, window, criteria) → retval, window¶
-
C:
cvCamShift(const CvArr* prob_image, CvRect window, CvTermCriteria criteria, CvConnectedComp* comp, CvBox2D* box=NULL )¶
-
Python:
cv.CamShift(prob_image, window, criteria) -> (int, comp, box)¶ Parameters: - probImage – Back projection of the object histogram. See
calcBackProject(). - window – Initial search window.
- criteria – Stop criteria for the underlying
meanShift().
Returns: (in old interfaces) Number of iterations CAMSHIFT took to converge
- probImage – Back projection of the object histogram. See
The function implements the CAMSHIFT object tracking algorithm
[Bradski98].
First, it finds an object center using
meanShift() and then adjusts the window size and finds the optimal rotation. The function returns the rotated rectangle structure that includes the object position, size, and orientation. The next position of the search window can be obtained with RotatedRect::boundingRect() .
See the OpenCV sample camshiftdemo.c that tracks colored objects.
Note
- (Python) A sample explaining the camshift tracking algorithm can be found at opencv_source_code/samples/python2/camshift.py
meanShift¶
Finds an object on a back projection image.
-
C++:
meanShift(InputArray probImage, Rect& window, TermCriteria criteria)¶
-
Python:
cv2.meanShift(probImage, window, criteria) → retval, window¶
-
C:
cvMeanShift(const CvArr* prob_image, CvRect window, CvTermCriteria criteria, CvConnectedComp* comp)¶
-
Python:
cv.MeanShift(prob_image, window, criteria) → comp¶ Parameters: - probImage – Back projection of the object histogram. See
calcBackProject()for details. - window – Initial search window.
- criteria – Stop criteria for the iterative search algorithm.
Returns: Number of iterations CAMSHIFT took to converge.
- probImage – Back projection of the object histogram. See
The function implements the iterative object search algorithm. It takes the input back projection of an object and the initial position. The mass center in window of the back projection image is computed and the search window center shifts to the mass center. The procedure is repeated until the specified number of iterations criteria.maxCount is done or until the window center shifts by less than criteria.epsilon . The algorithm is used inside
CamShift() and, unlike
CamShift() , the search window size or orientation do not change during the search. You can simply pass the output of
calcBackProject() to this function. But better results can be obtained if you pre-filter the back projection and remove the noise. For example, you can do this by retrieving connected components with
findContours() , throwing away contours with small area (
contourArea() ), and rendering the remaining contours with
drawContours() .
Note
- A mean-shift tracking sample can be found at opencv_source_code/samples/cpp/camshiftdemo.cpp
KalmanFilter¶
-
class
KalmanFilter¶ Kalman filter class.
The class implements a standard Kalman filter
http://en.wikipedia.org/wiki/Kalman_filter, [Welch95]. However, you can modify transitionMatrix, controlMatrix, and measurementMatrix to get an extended Kalman filter functionality. See the OpenCV sample kalman.cpp .
Note
- An example using the standard Kalman filter can be found at opencv_source_code/samples/cpp/kalman.cpp
KalmanFilter::KalmanFilter¶
The constructors.
-
C++:
KalmanFilter::KalmanFilter()¶
-
C++:
KalmanFilter::KalmanFilter(int dynamParams, int measureParams, int controlParams=0, int type=CV_32F)¶
-
Python:
cv2.KalmanFilter([dynamParams, measureParams[, controlParams[, type]]]) → <KalmanFilter object>¶
-
C:
cvCreateKalman(int dynam_params, int measure_params, int control_params=0 )¶
-
Python:
cv.CreateKalman(dynam_params, measure_params, control_params=0) → CvKalman¶ The full constructor.
Parameters: - dynamParams – Dimensionality of the state.
- measureParams – Dimensionality of the measurement.
- controlParams – Dimensionality of the control vector.
- type – Type of the created matrices that should be
CV_32ForCV_64F.
Note
In C API when CvKalman* kalmanFilter structure is not needed anymore, it should be released with cvReleaseKalman(&kalmanFilter)
KalmanFilter::init¶
Re-initializes Kalman filter. The previous content is destroyed.
-
C++:
KalmanFilter::init(int dynamParams, int measureParams, int controlParams=0, int type=CV_32F)¶ Parameters: - dynamParams – Dimensionalityensionality of the state.
- measureParams – Dimensionality of the measurement.
- controlParams – Dimensionality of the control vector.
- type – Type of the created matrices that should be
CV_32ForCV_64F.
KalmanFilter::predict¶
Computes a predicted state.
-
C++:
KalmanFilter::predict(const Mat& control=Mat())¶
-
Python:
cv2.KalmanFilter.predict([control]) → retval¶
-
C:
cvKalmanPredict(CvKalman* kalman, const CvMat* control=NULL)¶
-
Python:
cv.KalmanPredict(kalman, control=None) → mat¶ Parameters: control – The optional input control
KalmanFilter::correct¶
Updates the predicted state from the measurement.
-
C++:
KalmanFilter::correct(const Mat& measurement)¶
-
Python:
cv2.KalmanFilter.correct(measurement) → retval¶
-
C:
cvKalmanCorrect(CvKalman* kalman, const CvMat* measurement)¶
-
Python:
cv.KalmanCorrect(kalman, measurement) → mat¶ Parameters: measurement – The measured system parameters
BackgroundSubtractor¶
-
class
BackgroundSubtractor: publicAlgorithm¶
Base class for background/foreground segmentation.
class BackgroundSubtractor : public Algorithm
{
public:
virtual ~BackgroundSubtractor();
virtual void operator()(InputArray image, OutputArray fgmask, double learningRate=0);
virtual void getBackgroundImage(OutputArray backgroundImage) const;
};
The class is only used to define the common interface for the whole family of background/foreground segmentation algorithms.
BackgroundSubtractor::operator()¶
Computes a foreground mask.
-
C++:
BackgroundSubtractor::operator()(InputArray image, OutputArray fgmask, double learningRate=0)¶
-
Python:
cv2.BackgroundSubtractor.apply(image[, fgmask[, learningRate]]) → fgmask¶ Parameters: - image – Next video frame.
- fgmask – The output foreground mask as an 8-bit binary image.
BackgroundSubtractor::getBackgroundImage¶
Computes a background image.
-
C++:
BackgroundSubtractor::getBackgroundImage(OutputArray backgroundImage)const¶ Parameters: - backgroundImage – The output background image.
Note
Sometimes the background image can be very blurry, as it contain the average background statistics.
BackgroundSubtractorMOG¶
-
class
BackgroundSubtractorMOG: publicBackgroundSubtractor¶
Gaussian Mixture-based Background/Foreground Segmentation Algorithm.
The class implements the algorithm described in P. KadewTraKuPong and R. Bowden, An improved adaptive background mixture model for real-time tracking with shadow detection, Proc. 2nd European Workshop on Advanced Video-Based Surveillance Systems, 2001: http://personal.ee.surrey.ac.uk/Personal/R.Bowden/publications/avbs01/avbs01.pdf
BackgroundSubtractorMOG::BackgroundSubtractorMOG¶
The constructors.
-
C++:
BackgroundSubtractorMOG::BackgroundSubtractorMOG()¶
-
C++:
BackgroundSubtractorMOG::BackgroundSubtractorMOG(int history, int nmixtures, double backgroundRatio, double noiseSigma=0)¶
-
Python:
cv2.BackgroundSubtractorMOG([history, nmixtures, backgroundRatio[, noiseSigma]]) → <BackgroundSubtractorMOG object>¶ Parameters: - history – Length of the history.
- nmixtures – Number of Gaussian mixtures.
- backgroundRatio – Background ratio.
- noiseSigma – Noise strength.
Default constructor sets all parameters to default values.
BackgroundSubtractorMOG::operator()¶
Updates the background model and returns the foreground mask
-
C++:
BackgroundSubtractorMOG::operator()(InputArray image, OutputArray fgmask, double learningRate=0)¶
Parameters are the same as in BackgroundSubtractor::operator()
BackgroundSubtractorMOG2¶
Gaussian Mixture-based Background/Foreground Segmentation Algorithm.
-
class
BackgroundSubtractorMOG2: publicBackgroundSubtractor¶ Here are important members of the class that control the algorithm, which you can set after constructing the class instance:
-
int
nmixtures¶ Maximum allowed number of mixture components. Actual number is determined dynamically per pixel.
-
float
backgroundRatio¶ Threshold defining whether the component is significant enough to be included into the background model ( corresponds to
TB=1-cffrom the paper??which paper??).cf=0.1 => TB=0.9is default. Foralpha=0.001, it means that the mode should exist for approximately 105 frames before it is considered foreground.
-
float
varThresholdGen¶ Threshold for the squared Mahalanobis distance that helps decide when a sample is close to the existing components (corresponds to
Tg). If it is not close to any component, a new component is generated.3 sigma => Tg=3*3=9is default. A smallerTgvalue generates more components. A higherTgvalue may result in a small number of components but they can grow too large.
-
float
fVarInit¶ Initial variance for the newly generated components. It affects the speed of adaptation. The parameter value is based on your estimate of the typical standard deviation from the images. OpenCV uses 15 as a reasonable value.
-
float
fVarMin¶ Parameter used to further control the variance.
-
float
fVarMax¶ Parameter used to further control the variance.
-
float
fCT¶ Complexity reduction parameter. This parameter defines the number of samples needed to accept to prove the component exists.
CT=0.05is a default value for all the samples. By settingCT=0you get an algorithm very similar to the standard Stauffer&Grimson algorithm.
-
uchar
nShadowDetection¶ The value for marking shadow pixels in the output foreground mask. Default value is 127.
-
float
fTau¶ Shadow threshold. The shadow is detected if the pixel is a darker version of the background.
Tauis a threshold defining how much darker the shadow can be.Tau= 0.5means that if a pixel is more than twice darker then it is not shadow. See Prati,Mikic,Trivedi,Cucchiarra, Detecting Moving Shadows..., IEEE PAMI,2003.
-
int
The class implements the Gaussian mixture model background subtraction described in:
- Z.Zivkovic, Improved adaptive Gausian mixture model for background subtraction, International Conference Pattern Recognition, UK, August, 2004, http://www.zoranz.net/Publications/zivkovic2004ICPR.pdf. The code is very fast and performs also shadow detection. Number of Gausssian components is adapted per pixel.
- Z.Zivkovic, F. van der Heijden, Efficient Adaptive Density Estimapion per Image Pixel for the Task of Background Subtraction, Pattern Recognition Letters, vol. 27, no. 7, pages 773-780, 2006. The algorithm similar to the standard Stauffer&Grimson algorithm with additional selection of the number of the Gaussian components based on: Z.Zivkovic, F.van der Heijden, Recursive unsupervised learning of finite mixture models, IEEE Trans. on Pattern Analysis and Machine Intelligence, vol.26, no.5, pages 651-656, 2004.
BackgroundSubtractorMOG2::BackgroundSubtractorMOG2¶
The constructors.
-
C++:
BackgroundSubtractorMOG2::BackgroundSubtractorMOG2()¶
-
C++:
BackgroundSubtractorMOG2::BackgroundSubtractorMOG2(int history, float varThreshold, bool bShadowDetection=true )¶ Parameters: - history – Length of the history.
- varThreshold – Threshold on the squared Mahalanobis distance to decide whether it is well described by the background model (see Cthr??). This parameter does not affect the background update. A typical value could be 4 sigma, that is,
varThreshold=4*4=16;(see Tb??). - bShadowDetection – Parameter defining whether shadow detection should be enabled (
trueorfalse).
BackgroundSubtractorMOG2::operator()¶
Updates the background model and computes the foreground mask
-
C++:
BackgroundSubtractorMOG2::operator()(InputArray image, OutputArray fgmask, double learningRate=-1)¶
BackgroundSubtractorMOG2::getBackgroundImage¶
Returns background image
-
C++:
BackgroundSubtractorMOG2::getBackgroundImage(OutputArray backgroundImage)¶
calcOpticalFlowSF¶
Calculate an optical flow using “SimpleFlow” algorithm.
-
C++:
calcOpticalFlowSF(Mat& from, Mat& to, Mat& flow, int layers, int averaging_block_size, int max_flow)¶
-
C++:
calcOpticalFlowSF(Mat& from, Mat& to, Mat& flow, int layers, int averaging_block_size, int max_flow, double sigma_dist, double sigma_color, int postprocess_window, double sigma_dist_fix, double sigma_color_fix, double occ_thr, int upscale_averaging_radius, double upscale_sigma_dist, double upscale_sigma_color, double speed_up_thr)¶ Parameters: - prev – First 8-bit 3-channel image.
- next – Second 8-bit 3-channel image
- flowX – X-coordinate of estimated flow
- flowY – Y-coordinate of estimated flow
- layers – Number of layers
- averaging_block_size – Size of block through which we sum up when calculate cost function for pixel
- max_flow – maximal flow that we search at each level
- sigma_dist – vector smooth spatial sigma parameter
- sigma_color – vector smooth color sigma parameter
- postprocess_window – window size for postprocess cross bilateral filter
- sigma_dist_fix – spatial sigma for postprocess cross bilateralf filter
- sigma_color_fix – color sigma for postprocess cross bilateral filter
- occ_thr – threshold for detecting occlusions
- upscale_averaging_radiud – window size for bilateral upscale operation
- upscale_sigma_dist – spatial sigma for bilateral upscale operation
- upscale_sigma_color – color sigma for bilateral upscale operation
- speed_up_thr – threshold to detect point with irregular flow - where flow should be recalculated after upscale
See [Tao2012]. And site of project - http://graphics.berkeley.edu/papers/Tao-SAN-2012-05/.
Note
- An example using the simpleFlow algorithm can be found at opencv_source_code/samples/cpp/simpleflow_demo.cpp
createOptFlow_DualTVL1¶
“Dual TV L1” Optical Flow Algorithm.
-
C++:
createOptFlow_DualTVL1()¶ The class implements the “Dual TV L1” optical flow algorithm described in [Zach2007] and [Javier2012] .
Here are important members of the class that control the algorithm, which you can set after constructing the class instance:
-
double
tau¶ Time step of the numerical scheme.
-
double
lambda¶ Weight parameter for the data term, attachment parameter. This is the most relevant parameter, which determines the smoothness of the output. The smaller this parameter is, the smoother the solutions we obtain. It depends on the range of motions of the images, so its value should be adapted to each image sequence.
-
double
theta¶ Weight parameter for (u - v)^2, tightness parameter. It serves as a link between the attachment and the regularization terms. In theory, it should have a small value in order to maintain both parts in correspondence. The method is stable for a large range of values of this parameter.
-
int
nscales¶ Number of scales used to create the pyramid of images.
-
int
warps¶ Number of warpings per scale. Represents the number of times that I1(x+u0) and grad( I1(x+u0) ) are computed per scale. This is a parameter that assures the stability of the method. It also affects the running time, so it is a compromise between speed and accuracy.
-
double
epsilon¶ Stopping criterion threshold used in the numerical scheme, which is a trade-off between precision and running time. A small value will yield more accurate solutions at the expense of a slower convergence.
-
int
iterations¶ Stopping criterion iterations number used in the numerical scheme.
-
double
DenseOpticalFlow::calc¶
Calculates an optical flow.
-
C++:
DenseOpticalFlow::calc(InputArray I0, InputArray I1, InputOutputArray flow)¶ Parameters: - prev – first 8-bit single-channel input image.
- next – second input image of the same size and the same type as
prev. - flow – computed flow image that has the same size as
prevand typeCV_32FC2.
DenseOpticalFlow::collectGarbage¶
Releases all inner buffers.
-
C++:
DenseOpticalFlow::collectGarbage()¶
| [Bouguet00] | (1, 2) Jean-Yves Bouguet. Pyramidal Implementation of the Lucas Kanade Feature Tracker. |
| [Bradski98] | Bradski, G.R. “Computer Vision Face Tracking for Use in a Perceptual User Interface”, Intel, 1998 |
| [Bradski00] | Davis, J.W. and Bradski, G.R. “Motion Segmentation and Pose Recognition with Motion History Gradients”, WACV00, 2000 |
| [Davis97] | Davis, J.W. and Bobick, A.F. “The Representation and Recognition of Action Using Temporal Templates”, CVPR97, 1997 |
| [Farneback2003] | Gunnar Farneback, Two-frame motion estimation based on polynomial expansion, Lecture Notes in Computer Science, 2003, (2749), , 363-370. |
| [Horn81] | Berthold K.P. Horn and Brian G. Schunck. Determining Optical Flow. Artificial Intelligence, 17, pp. 185-203, 1981. |
| [Lucas81] | Lucas, B., and Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision, Proc. of 7th International Joint Conference on Artificial Intelligence (IJCAI), pp. 674-679. |
| [Welch95] | Greg Welch and Gary Bishop “An Introduction to the Kalman Filter”, 1995 |
| [Tao2012] | Michael Tao, Jiamin Bai, Pushmeet Kohli and Sylvain Paris. SimpleFlow: A Non-iterative, Sublinear Optical Flow Algorithm. Computer Graphics Forum (Eurographics 2012) |
| [Zach2007] |
|
| [Javier2012] | Javier Sanchez, Enric Meinhardt-Llopis and Gabriele Facciolo. “TV-L1 Optical Flow Estimation”. |
Help and Feedback
You did not find what you were looking for?- Ask a question on the Q&A forum.
- If you think something is missing or wrong in the documentation, please file a bug report.
![[A^*|b^*] = arg \min _{[A|b]} \sum _i \| \texttt{dst}[i] - A { \texttt{src}[i]}^T - b \| ^2](../../../_images/math/f8a14dd7db6d05574d1b960fe9f1e72bf48adf77.png)